题目内容
点P为椭圆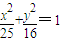 上的动点,F1,F2为椭圆的左、右焦点,则
上的动点,F1,F2为椭圆的左、右焦点,则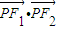 的最小值为 ,此时点P的坐标为 .
的最小值为 ,此时点P的坐标为 .
【答案】分析:先根据椭圆方程求出焦点坐标,再设点P的坐标为(5cost,4sint).表示出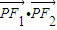 根据三角函数的性质求得最小值,进而可求得此时t的值,进而可得点P此时的坐标.
根据三角函数的性质求得最小值,进而可求得此时t的值,进而可得点P此时的坐标.
解答:解:易知,F1(-3,0),F2(3,0).可设点P(5cost,4sint).
则 =(-3-5cost,-4sint)•(3-5cost,-4sint)=25cos2t-9+16sin2t=9cos2t+7≥7.
=(-3-5cost,-4sint)•(3-5cost,-4sint)=25cos2t-9+16sin2t=9cos2t+7≥7.
∴当t=kπ时,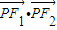 的最小值为7,则点P的坐标为(0,±4)
的最小值为7,则点P的坐标为(0,±4)
故答案为7,(0,±4)
点评:本题主要考查了椭圆的应用.由于椭圆方程的特殊性,对于求最值问题可利用极坐标的形式,利用三角函数的性质来解决.
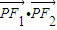 根据三角函数的性质求得最小值,进而可求得此时t的值,进而可得点P此时的坐标.
根据三角函数的性质求得最小值,进而可求得此时t的值,进而可得点P此时的坐标.解答:解:易知,F1(-3,0),F2(3,0).可设点P(5cost,4sint).
则
 =(-3-5cost,-4sint)•(3-5cost,-4sint)=25cos2t-9+16sin2t=9cos2t+7≥7.
=(-3-5cost,-4sint)•(3-5cost,-4sint)=25cos2t-9+16sin2t=9cos2t+7≥7.∴当t=kπ时,
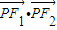 的最小值为7,则点P的坐标为(0,±4)
的最小值为7,则点P的坐标为(0,±4)故答案为7,(0,±4)
点评:本题主要考查了椭圆的应用.由于椭圆方程的特殊性,对于求最值问题可利用极坐标的形式,利用三角函数的性质来解决.

练习册系列答案
相关题目