Question

【题目】函数的部分图象如图所示．

（Ⅰ）写出及图中的值．

（Ⅱ）设，求函数在区间上的最大值和最小值．

Answer 1

【答案】（Ⅰ）， ．（Ⅱ）最大值，最小值．

【解析】试题分析：（1）将点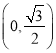代入，由已给条件可求得；由并结合图象可求得.

（2）由（1）可得到，由，得，可得在和时，函数分别取得最大值和最小值。

试题解析：（Ⅰ）∵图象过点，∴，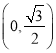

又，∴，

由，得或， ，

又的周期为，结合图象知，∴．

（Ⅱ）由题意可得，

∴

，

∵，

∴，

∴当，即时， 取得最大值，

当，即时， 取得最小值．

点睛:　三角函数式的化简要遵循“三看”原则

（1）一看“角”，这是最重要的一环，通过看角之间的区别和联系，把角进行合理的拆分，从而正确使用公式；

（2）而看“函数名称”看函数名称之间的差异，从而确定使用公式，常见的有“切化弦”；

（3）三看“结构特征”，分析结构特征，可以帮助我们找到变形的方向，如“遇到分式通分”等.