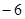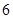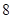题目内容
设函数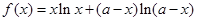
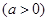 .
.
(1)当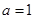 时,求函数
时,求函数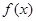 的最小值;
的最小值;
(2)证明:对 ,都有
,都有 ;
;
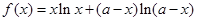
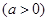 .
.(1)当
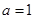 时,求函数
时,求函数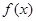 的最小值;
的最小值;(2)证明:对
 ,都有
,都有 ;
;(1)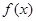 在
在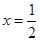 时取得最小值,即
时取得最小值,即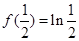 .
.
(2)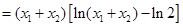
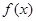 在
在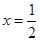 时取得最小值,即
时取得最小值,即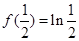 .
.(2)
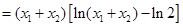
(1)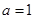 时,
时,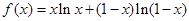 ,(
,(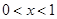 ),
),
则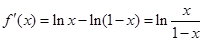 .令
.令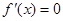 ,得
,得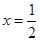 .
.
当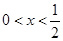 时,
时,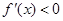 ,
,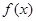 在
在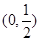 是减函数,
是减函数,
当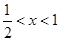 时,
时,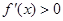 ,
,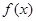 在
在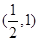 是增函数,
是增函数,
所以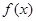 在
在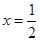 时取得最小值,即
时取得最小值,即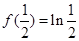 . (6分)
. (6分)
(2)因为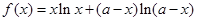 ,所以
,所以 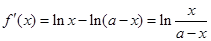 .
.
所以当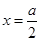 时,函数
时,函数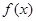 有最小值.
有最小值.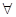 x1,x2∈R+,不妨设
x1,x2∈R+,不妨设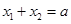 ,则
,则

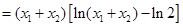 . (13分)
. (13分)
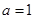 时,
时,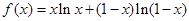 ,(
,(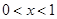 ),
),则
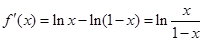 .令
.令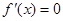 ,得
,得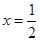 .
.当
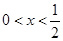 时,
时,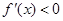 ,
,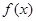 在
在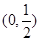 是减函数,
是减函数,当
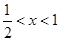 时,
时,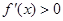 ,
,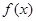 在
在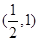 是增函数,
是增函数, 所以
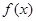 在
在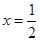 时取得最小值,即
时取得最小值,即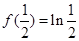 . (6分)
. (6分)(2)因为
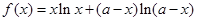 ,所以
,所以 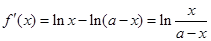 .
. 所以当
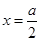 时,函数
时,函数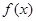 有最小值.
有最小值.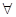 x1,x2∈R+,不妨设
x1,x2∈R+,不妨设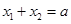 ,则
,则
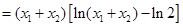 . (13分)
. (13分)
练习册系列答案
相关题目
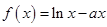 .
.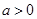 时,求函数
时,求函数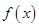 在区间
在区间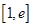 内的最大值;
内的最大值;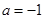 时,方程
时,方程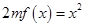 有唯一实数解,求正数
有唯一实数解,求正数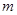 的值.
的值. 满足:
满足: 记y=f(x).
记y=f(x). 不等式
不等式 恒成立,求实数a的取值范围:
恒成立,求实数a的取值范围: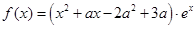 ,其中
,其中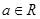 .
.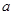 ,使得函数
,使得函数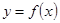 在
在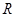 上单调递增?若存在,求出的
上单调递增?若存在,求出的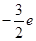 ,求函数的极大值。
,求函数的极大值。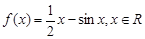 .
.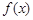 的递减区间;
的递减区间;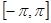 上的最值.
上的最值.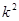 ,若
,若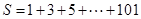 ( )
( )
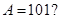
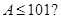
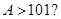
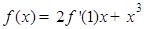 ,则
,则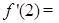 ( )
( )