题目内容
若函数f（x）=loga（x2-ax+
）有最小值，则实数a的取值范围是
- A.（0，1）
- B.（0，1）∪（1，
） - C.（1，）
- D.[，+∞）
C
分析：令u=x2-ax+=
+-
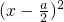，则u有最小值，欲满足题意，须logau递增，且u的最小值-＞0，由此可求a的范围．
解答：令u=x2-ax+=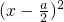+-，则u有最小值-，
欲使函数f（x）=loga（x2-ax+）有最小值，则须有
，解得1＜a＜．
即a的取值范围为（1，）．
故选C．
点评：本题考查复合函数的单调性，若复合函数可分解为两个基本初等函数，依据“同增异减”即可判断复合函数的单调性．
分析：令u=x2-ax+
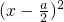=+-，则u有最小值，欲满足题意，须logau递增，且u的最小值-＞0，由此可求a的范围．解答：令u=x2-ax+
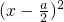=+-，则u有最小值-，欲使函数f（x）=loga（x2-ax+
）有最小值，则须有，解得1＜a＜．即a的取值范围为（1，
）．故选C．
点评：本题考查复合函数的单调性，若复合函数可分解为两个基本初等函数，依据“同增异减”即可判断复合函数的单调性．
练习册系列答案
阅读快车系列答案
相关题目
的定义域为M，g(x)＝lo
(2＋x＝6x2)的单调递减区间是开区间N，设全集U＝R，则M∩CU(N)＝________．
(x2－2ax＋3)．
(m∈R)
[8－f(x)]在[1，＋∞)上是单调减函数，求实数m的取值范围；
上的最大值．
的奇函数，a为常数，
)x＋m恒成立，求实数m的取值范围．