题目内容
1．已知函数$f（x）=\frac{1}{x}-{log_2}\frac{2+x}{2-x}$．（1）求f（x）的定义域；
（2）判断并证明f（x）的奇偶性．
分析 （1）根据函数成立的条件建立不等式关系即可求出函数的定义域．
（2）根据函数奇偶性的定义进行判断即可．
解答 解：（1）函数f（x）有意义，需$\left\{\begin{array}{l}x≠0\\ \frac{2+x}{2-x}＞0\end{array}\right.$，得-2＜x＜2且x≠0，
∴函数定义域为{x|-2＜x＜0或0＜x＜2}．…（6分）
（2）函数f（x）为奇函数，
∵$f（x）=\frac{1}{x}-{log_2}\frac{2+x}{2-x}=-\frac{1}{x}+{log_2}\frac{2+x}{2-x}=-f（x）$，
又由（1）已知f（x）的定义域关于原点对称，
∴f（x）为奇函数．…（12分）
点评 本题主要考查函数定义域和函数奇偶性的判断，根据函数奇偶性的定义是解决本题的关键．
练习册系列答案
相关题目
11．不等式$\frac{1}{x-1}$≥-1的解集为（ ）
| A． | （-∞，0]∪（1，+∞） | B． | （-∞，0）∪[1，+∞） | C． | （0，1] | D． | [0，1） |
12．设命题p：?x＞1，x2-x+1＞0，则?p为（ ）
| A． | ?x≤1，x2-x+1≤0 | B． | ?x＞1，x2-x+1≤0 | C． | ?x＞1，x2-x+1≤0 | D． | ?x≤1，x2-x+1＞0 |
9．函数y=lg（-x2-2x+8）的单调递减区间是（ ）
| A． | （-∞，-1） | B． | （-1，2） | C． | （-4，-1） | D． | （-1，+∞） |
16．
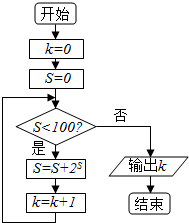如果执行如图所示的程序，那么输出的值k=（ ）
如果执行如图所示的程序，那么输出的值k=（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |