题目内容
4．在（a+b）n的二项展开式中，若奇数项的二项式系数的和为128，则二项式系数的最大值为70（结果用数字作答）．分析 利用二项展开式的二项式系数的性质：二项式系数和为2n，展开式中中间项的二项式系数最大．
解答 解：在（a+b）n的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和，
∴2n=256，
解得n=8，
展开式共n+1=8+1=9项，
据中间项的二项式系数最大，
故展开式中系数最大的项是第5项，最大值为${C}_{8}^{4}$=70．
故答案为：70．
点评 本题考查二项展开式的二项式系数的性质：二项式系数和是2n；展开式中中间项的二项式系数最大．在（a+b）n的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和．
练习册系列答案
阅读快车系列答案
相关题目
15．下列判断错误的是（ ）
| A． | “am2＜bm2”是“a＜b”的充分不必要条件 | |
| B． | 命题“?x∈R，x3-x2≤0”的否定是“?x∈R，x3-x2-1＞0” | |
| C． | “若a=1，则直线x+y=0和直线x-ay=0互相垂直”的逆否命题为真命题 | |
| D． | 若p∧q为假命题，则p，q均为假命题 |
19．下列有关命题的叙述错误的是（ ）
| A． | 若非p是q的必要条件，则p是非q的充分条件 | |
| B． | “x＞2”是“$\frac{1}{x}＜\frac{1}{2}$”的充分不必要条件 | |
| C． | 命题“?x∈R，x2-x≥0”的否定是“?x∈R，x2-x＜0” | |
| D． | 若p且q为假命题，则p，q均为假命题 |
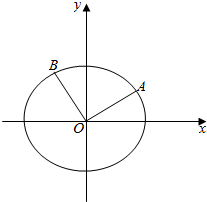如图，已知点A是单位圆上一点，且位于第一象限，以x轴的正半轴为始边，OA为终边的角设为α，将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB．
16．已知复数z，“z+$\overline{z}$=0”是“z为纯虚数”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既非充分也不必要条件 |