题目内容
已知各项为正数的等差数列{an}满足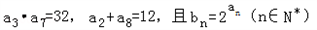 .
.
(I)求数列{an}的通项公式;
(II)设cn=an+bn,求数列{cn}的前n项和Sn.
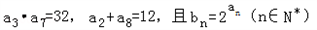 .
.(I)求数列{an}的通项公式;
(II)设cn=an+bn,求数列{cn}的前n项和Sn.
解:(I)(方法一)设等差数列{an}的公差为d
则
联立方程,消去a1可得,9﹣d2=8
∴d2=1∴d=±1
由an>0可知公差d>0
∴d=1∴a1=2∴an=n+1
(方法二)∵数列{an}是等差数列
由等差数列的性质可得,a2+a8=a3+a7=12
∴a3a7=32
∴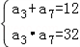 解方程可得,
解方程可得,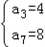 或
或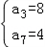
∵an>0
∴d>0,
∴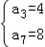
由等差数列的通项公式可得,d=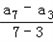 =
=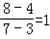
等差数列的通项公式为:an=a3+(n﹣3)d=n+1
(II)由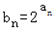 =2n+1
=2n+1
∴cn=an+bn=n+1+2n+1
∴Sn=c1+c2+…+cn=(a1+a2+…+an)+(b1+b2+…+bn)
=[2+3+…+(n+1)]+(22+23+…+2n+1)
=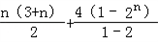
=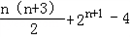

练习册系列答案
相关题目
已知{an}为各项均为正数的等比数列,Sn是它的前n项和,若a2•a3=2a1,且a4与a6的等差中项为
,则S4=( )
| 5 |
| 4 |
| A、35 | B、33 | C、30 | D、29 |
 满足
满足 (
( ),且
),且 是
是 的等差中项,则数列
的等差中项,则数列 满足
满足 ,且
,且 是
是 的等差中项.
的等差中项.  ;
; ,求使
,求使 成立的正整数n的最小值.
成立的正整数n的最小值.