题目内容
已知各项为正数的数列 满足
满足 ,且
,且 是
是 的等差中项.
的等差中项.
(1)求数列 的通项公式
的通项公式 ;
;
(2)若 ,求使
,求使 成立的正整数n的最小值.
成立的正整数n的最小值.
【答案】
(1)∵
∴ ,∵数列
,∵数列 的各项均为正数,………………2分
的各项均为正数,………………2分
∴ ,∴
,∴ ,即
,即 (n∈N
(n∈N ),所以数列
),所以数列 是以2为公比的等比数列.
……………4分
是以2为公比的等比数列.
……………4分
∵ 的等差中项,∴
的等差中项,∴ ,
,
∴ ,∴a1=2,∴数列
,∴a1=2,∴数列 的通项公式
的通项公式 .………6分
.………6分
(2)由(1)及 ,得
,得 ,
,
∵ ,
,
∴ , ①…………8分
, ①…………8分
∴ ②
②
①-②得,
 .
…………10分
.
…………10分
要使 成立,只需
成立,只需 成立,即
成立,即
∴使 成立的正整数n的最小值为5.
…………12分
成立的正整数n的最小值为5.
…………12分

练习册系列答案
相关题目
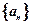 的前
的前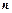 项和为
项和为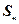 ,且满足
,且满足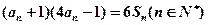 ,
,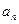
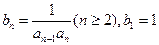 ,数列
,数列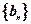 的前
的前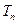 ,若
,若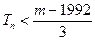 对一切
对一切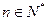 恒成立,求
恒成立,求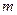 的最小值.
的最小值.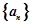 的前
的前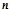 项和为
项和为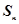 ,且满足
,且满足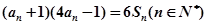 ,
,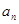
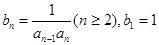 ,数列
,数列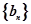 的前
的前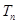 ,若
,若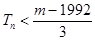 对一切
对一切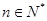 恒成立,求
恒成立,求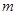 的最小值.
的最小值.