题目内容
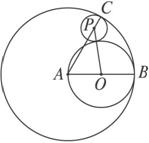
如图,
⊙ 与⊙O外切于点C,连心线
与⊙O外切于点C,连心线 所在的直线分别交⊙
所在的直线分别交⊙ 、⊙O于点A与点E,过点A画⊙O的切线AD交⊙
、⊙O于点A与点E,过点A画⊙O的切线AD交⊙ 于点B,切点为D,过点E画⊙O的切线EF与AD的延长线交于点F,连结BC、CD、DE.
于点B,切点为D,过点E画⊙O的切线EF与AD的延长线交于点F,连结BC、CD、DE.

(1)
如果 ,求
,求 的值.
的值.
(2)
在(1)的条件下,求sinA与tan∠DCE的值.(3)
在 为何值时,△DEF是正三角形.
为何值时,△DEF是正三角形.
答案:略
解析:
提示:
解析:
|
解: (1)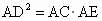 ,又∵ ,又∵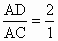 ,设AC=k, ,设AC=k,
∴AD=2k ,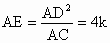 .∴CE=3k,∴ .∴CE=3k,∴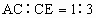 . .
(2) 连结DO,则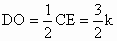 , ,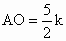 .又∵OD⊥AD,∴ .又∵OD⊥AD,∴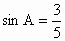 . .
又 ∵∠A=∠A,∠ADC=∠AED,∴△ACD∽△ADE.∴ 又 ∵∠CDE=90°,∴tan∠DCE=2.(3) 当△DEF为正三角形时,∠DCE=∠DEF=60°,∴ . .
∵△ACD∽△ADE .∴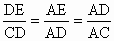 , ,
∴ 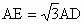 . .
又 ∵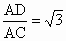 ,∴ ,∴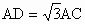 . .
∴ ∴ |
提示:
|
分析:(1)由AD、ACE为⊙O的切线与割线,利用切割线定理得(1),解直角三角形可得(2),对于(3)假设△DEF为正三角形,求AC∶CE的值,即逆向思维. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
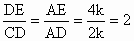
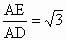
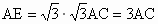
 选做题:考生在下面两小题中,任选一道作答,如果全做则按第1小题评分.
选做题:考生在下面两小题中,任选一道作答,如果全做则按第1小题评分.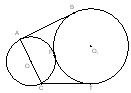 (附加题-选做题)(几何证明选讲)
(附加题-选做题)(几何证明选讲)