题目内容
如图,AB是⊙A的半径,又是⊙O的直径,⊙P内切⊙A于C,且与⊙O外切,∠CAB=60°,求AP∶PC的值.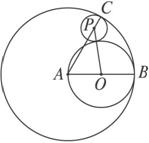
解:设⊙A半径为R,
由题意知⊙O半径为
,设⊙P半径为r,
则根据圆的位置关系,PO=
+r,AP=R-r,AO=
.
在△AOP中,应用余弦定理cosA=
,
即cos60°=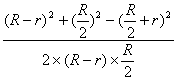
,
解得R=5r,AP∶PC=(R-r)∶r=4∶1.
练习册系列答案
相关题目
题目内容
如图,AB是⊙A的半径,又是⊙O的直径,⊙P内切⊙A于C,且与⊙O外切,∠CAB=60°,求AP∶PC的值.
解:设⊙A半径为R,
由题意知⊙O半径为,设⊙P半径为r,
则根据圆的位置关系,PO=+r,AP=R-r,AO=.
在△AOP中,应用余弦定理cosA=,
即cos60°=,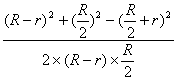
解得R=5r,AP∶PC=(R-r)∶r=4∶1.
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．请在答题纸指定区域内 作答．解答应写出文字说明、证明过程或演算步骤．
[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
如图，直角△ABC的顶点A、B分别在x轴、y轴的正半轴上移动，直角顶点C与原点O在直线AB的两侧，则顶点C的轨迹是 （ ）
如图，
是⊙O的直径，弦
、
的延长线相交于点E，EF垂直BA的延长线于点F．求证：
；
．
在矩阵MN对应的变换作用下得到的曲线方程，其中
，
．
，曲线C的参数方程为
，又直线l与曲线C交于A，B两点，求线段AB的长.
使
成立，求常数
的取值范围．