题目内容
(本小题满分12分)如图,已知斜三棱柱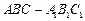 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成的角为
,侧棱与底面所成的角为 ,点
,点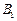 在底面上的射影
在底面上的射影 落在
落在 上.
上.

(1)若点 恰为
恰为 的中点,且
的中点,且 ,求
,求 的值.
的值.
(2)若 ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小.
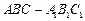 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成的角为
,侧棱与底面所成的角为 ,点
,点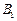 在底面上的射影
在底面上的射影 落在
落在 上.
上.
(1)若点
 恰为
恰为 的中点,且
的中点,且 ,求
,求 的值.
的值.(2)若
 ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小.(1)60°;(2)45°
(1) 面
面 ,
, ,又
,又
 面
面 .又
.又 ,由三垂线定理可知,
,由三垂线定理可知, ,即平行四边形
,即平行四边形 为菱形
为菱形

又 ,且
,且 为
为 的中点,
的中点,
 .即
.即 为正三角形,
为正三角形, ,
, 平面
平面 ,且点
,且点 落在
落在 上,
上, 即为侧棱与底面所成的角.
即为侧棱与底面所成的角.
 .
.
(2)过 ,垂足为
,垂足为 ,则
,则 平面
平面 .过
.过 作
作 ,垂足为
,垂足为 ,由三垂线定理得
,由三垂线定理得 .
. 是所求二面角
是所求二面角 的平面角.
的平面角.
设 ,在
,在 中,由
中,由 .
.
在
 . 故所求的二面角
. 故所求的二面角 为45°.
为45°.
 面
面 ,
, ,又
,又
 面
面 .又
.又 ,由三垂线定理可知,
,由三垂线定理可知, ,即平行四边形
,即平行四边形 为菱形
为菱形
又
 ,且
,且 为
为 的中点,
的中点,
 .即
.即 为正三角形,
为正三角形, ,
, 平面
平面 ,且点
,且点 落在
落在 上,
上, 即为侧棱与底面所成的角.
即为侧棱与底面所成的角.
 .
.(2)过
 ,垂足为
,垂足为 ,则
,则 平面
平面 .过
.过 作
作 ,垂足为
,垂足为 ,由三垂线定理得
,由三垂线定理得 .
. 是所求二面角
是所求二面角 的平面角.
的平面角. 设
 ,在
,在 中,由
中,由 .
.在

 . 故所求的二面角
. 故所求的二面角 为45°.
为45°.
练习册系列答案
相关题目

 ,
, 求证:MN⊥平面PCD.
求证:MN⊥平面PCD.
 与正三角形
与正三角形 组合而成的平面图形中,
组合而成的平面图形中, 现将正三角形
现将正三角形 折成四棱锥
折成四棱锥 ,使
,使 在平面
在平面 上.
上.

 ⊥平面
⊥平面 ;
; 与平面
与平面 关于
关于 轴对称点
轴对称点 的坐标为 .
的坐标为 .