题目内容
已知:函数 。
。
(1)判断函数f(x)的奇偶性;
(2)求f(x)的单调区间;
(3)若关于x的方程kf(x)=1恰有三个不同的根,求实数k的取值范围。
 。
。(1)判断函数f(x)的奇偶性;
(2)求f(x)的单调区间;
(3)若关于x的方程kf(x)=1恰有三个不同的根,求实数k的取值范围。
解:f(x)定义域为(-∞,0)∪(0,+∞)
(1)当x>0时,-x <0,
∵f(x)=xlnx,f(-x)=-xlnx,
∴f(-x)=- f(x),
当x<0时,-x >0,
∵f(x)= xln(-x),f(-x)=-xln(-x),
∴f(-x)=-f(x),
∴f(x)是奇函数。
(2)当x>0时,f(x)=xlnx,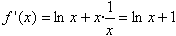
令f'(x)<0,得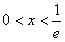
∴当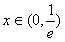 时,f(x)为减函数
时,f(x)为减函数
令f'(x)>0,得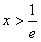
∴当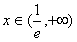 时,f(x)为增函数
时,f(x)为增函数
又f(x)为奇函数,
∴当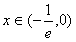 时,f(x)为减函数,
时,f(x)为减函数,
当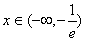 时,f(x)为增函数
时,f(x)为增函数
∴f(x)的单调减区间为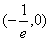 和
和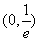
单调增区间为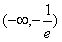 和
和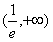 。
。
(3)原方程等价于 ,结合f(x)的图象变化,由(2)知,
,结合f(x)的图象变化,由(2)知,
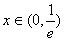 时f(x)由0递减到
时f(x)由0递减到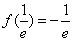
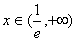 时f(x)由
时f(x)由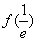 递增到+∞
递增到+∞
x∈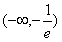 时f(x)由-∞递增到
时f(x)由-∞递增到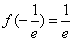
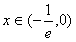 时f(x)由
时f(x)由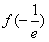 递减到0
递减到0
∵方程 恰有3个不同的根,
恰有3个不同的根,
∴f(x)的图象与 的图象应有3个不同的交点,
的图象应有3个不同的交点,
∴ 或
或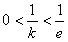
∴k<-e或k>e。
(1)当x>0时,-x <0,
∵f(x)=xlnx,f(-x)=-xlnx,
∴f(-x)=- f(x),
当x<0时,-x >0,
∵f(x)= xln(-x),f(-x)=-xln(-x),
∴f(-x)=-f(x),
∴f(x)是奇函数。
(2)当x>0时,f(x)=xlnx,
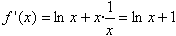
令f'(x)<0,得
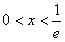
∴当
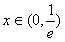 时,f(x)为减函数
时,f(x)为减函数令f'(x)>0,得
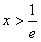
∴当
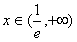 时,f(x)为增函数
时,f(x)为增函数又f(x)为奇函数,
∴当
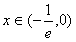 时,f(x)为减函数,
时,f(x)为减函数,当
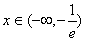 时,f(x)为增函数
时,f(x)为增函数∴f(x)的单调减区间为
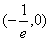 和
和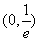
单调增区间为
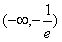 和
和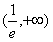 。
。(3)原方程等价于
 ,结合f(x)的图象变化,由(2)知,
,结合f(x)的图象变化,由(2)知,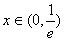 时f(x)由0递减到
时f(x)由0递减到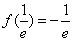
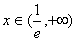 时f(x)由
时f(x)由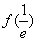 递增到+∞
递增到+∞ x∈
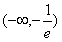 时f(x)由-∞递增到
时f(x)由-∞递增到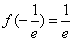
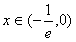 时f(x)由
时f(x)由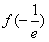 递减到0
递减到0∵方程
 恰有3个不同的根,
恰有3个不同的根, ∴f(x)的图象与
 的图象应有3个不同的交点,
的图象应有3个不同的交点,∴
 或
或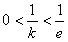
∴k<-e或k>e。

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目

 (理)已知函数
(理)已知函数