题目内容
已知不等式xy≤ax2+2y2,若对任意x∈[1,2]及y∈[2,3],该不等式恒成立,则实数a的范围是( )
A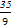．- ≤a≤-1 | B．-3≤a≤-1 |
| C．a≥-3 | D．a≥-1 |
D
将参数a分离到不等式的一边,然后求不等式另一边的最大值,令t=
,通过换元,转化为二次函数在闭区间上的最值问题.
由xy≤ax2+2y2可得a≥-2()2,令t=,g(t)=-2t2+t,由于x∈[1,2],y∈[2,3],所以t∈[1,3],于是g(t)=-2t2+t=-2(t-
)2+
,因此g(t)的最大值为g(1)=-1,故要使不等式恒成立,实数a的范围是a≥-1.
,通过换元,转化为二次函数在闭区间上的最值问题.由xy≤ax2+2y2可得a≥
-2()2,令t=,g(t)=-2t2+t,由于x∈[1,2],y∈[2,3],所以t∈[1,3],于是g(t)=-2t2+t=-2(t-)2+,因此g(t)的最大值为g(1)=-1,故要使不等式恒成立,实数a的范围是a≥-1.
练习册系列答案
阅读快车系列答案
相关题目
的定义域为R.
,解关于x的不等式x2-x-a2-a<0.
-
,n=
,则m,n的关系是 .
的不等式
对于一切实数
”的
+3与B=
+2,则A,B的大小关系是( )
对任意实数
恒成立，则实数
的取值范围为_________________