题目内容
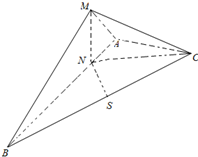 如图,在三棱锥M-ABC中,AB=2AC=2,MA=MB=
如图,在三棱锥M-ABC中,AB=2AC=2,MA=MB=
| ||
| 2 |
(1)证明:CM⊥SN;
(2)求SN与平面CMN所成角的大小.
分析:解法一:(1)向量法,取AB中点O,建立空间直角坐标系,用坐标表示点、向量,利用
•
=0,证明CM⊥SN;
(2)求出平面CMN的法向量、
,利用向量的夹角公式,即可求得SN与平面CMN所成角;
解法二:(1)取AB中点O,连接MO、CO、SO,利用平面MAB⊥平面ABC,证明MO⊥平面ABC,从而可证CM⊥SN;
(2)在△MNC中,利用等体积计算S到平面MNC的距离,即可求得SN与平面CMN所成角.
| CM |
| SN |
(2)求出平面CMN的法向量、
| SN |
解法二:(1)取AB中点O,连接MO、CO、SO,利用平面MAB⊥平面ABC,证明MO⊥平面ABC,从而可证CM⊥SN;
(2)在△MNC中,利用等体积计算S到平面MNC的距离,即可求得SN与平面CMN所成角.
解答:
解法一:(1)证明:取AB中点O,由题意,如图建立空间直角坐标系,各点坐标如下:C(-1,1,0)、M(0,0,
)、N(-
,0,0)、S(0,
,0)
∴
=(1,-1,
),
=(-
,-
,0)…(5分)
∴
•
=0,∴CM⊥SN…(6分)
(2)由题意知
=(
,-1,0),
=(
,0,
)…(8分)
设平面CMN的法向量为
=(x,y,z),则
,∴
平面CMN的法向量为
=(2,1,-2)…(10分)
∴|cos<
,
>|=
,∴SN与平面CMN所成角为
…(12分)
解法二:(1)取AB中点O,连接MO、CO、SO
∵MA=MB,∴MO⊥AB
∵平面MAB⊥平面ABC,平面MAB∩平面ABC=AB
∴MO⊥平面ABC…(2分)
∵△NOS和△AOC都是等腰直角三角形
∵AB=2AC=2,AB=4AN,
∴AO=CO,NO=SO,
∴∠AOC=45°,∠ONS=45°,
∴CO⊥SN,∴CM⊥SN…(6分)
(2)在△MNC中,MN=
CN=
CM=
,
∴S△MNC=
…(10分)
设S到平面MNC的距离为h,SN与平面CMN所成角为θ
∵VM-NSC=VS-NMC
∴S△NSC•MO=S△MNC•h
∴h=
…(11分)
∴sinθ=
=
∴SN与平面CMN所成角为
…(12分)

解法一:(1)证明:取AB中点O,由题意,如图建立空间直角坐标系,各点坐标如下:C(-1,1,0)、M(0,0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| CM |
| 1 |
| 2 |
| SN |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| CM |
| SN |
(2)由题意知
| CN |
| 1 |
| 2 |
| NM |
| 1 |
| 2 |
| 1 |
| 2 |
设平面CMN的法向量为
| n |
|
|
平面CMN的法向量为
| n |
∴|cos<
| n |
| SN |
| ||
| 2 |
| π |
| 4 |
解法二:(1)取AB中点O,连接MO、CO、SO

∵MA=MB,∴MO⊥AB
∵平面MAB⊥平面ABC,平面MAB∩平面ABC=AB
∴MO⊥平面ABC…(2分)
∵△NOS和△AOC都是等腰直角三角形
∵AB=2AC=2,AB=4AN,
∴AO=CO,NO=SO,
∴∠AOC=45°,∠ONS=45°,
∴CO⊥SN,∴CM⊥SN…(6分)
(2)在△MNC中,MN=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
∴S△MNC=
| 3 |
| 8 |
设S到平面MNC的距离为h,SN与平面CMN所成角为θ
∵VM-NSC=VS-NMC
∴S△NSC•MO=S△MNC•h
∴h=
| 1 |
| 2 |
∴sinθ=
| h |
| SN |
| ||
| 2 |
∴SN与平面CMN所成角为
| π |
| 4 |
点评:本题考查线线垂直,考查线面角,解题的关键是掌握线面垂直的判定,掌握线面角的求法,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
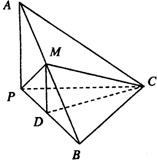 21、如图,在三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形,
21、如图,在三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形,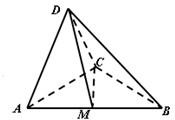 如图,在三棱锥D-ABC中,△ADC,△ACB均为等腰直角三角形AD=CD=
如图,在三棱锥D-ABC中,△ADC,△ACB均为等腰直角三角形AD=CD=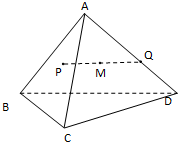 如图,在三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于
如图,在三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于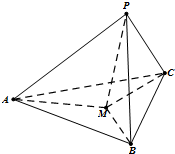 如图,在三棱锥P-ABC中,PA,PB,PC两两垂直,且PA=5,PB=4,PC=3.设点M为底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别为三棱锥M-PAB、M-PBC、M-PCA的体积.若f(M)=(4,3x,3y),且ax-8xy+y≥0恒成立,则正实数a的取值范围是
如图,在三棱锥P-ABC中,PA,PB,PC两两垂直,且PA=5,PB=4,PC=3.设点M为底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别为三棱锥M-PAB、M-PBC、M-PCA的体积.若f(M)=(4,3x,3y),且ax-8xy+y≥0恒成立,则正实数a的取值范围是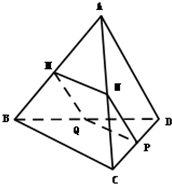 如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.
如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.