题目内容
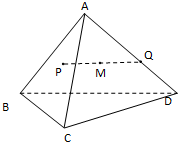 如图,在三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于
如图,在三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于分析:由已知中三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4,我们易计算出三棱锥A-BCD的体积,又由点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,我们可以判断M的轨迹与三棱锥转成的两个几何体的体积,进而得到答案.
解答:解:∵三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4,
则棱锥A-BCD的体积V=
×
×4×4×4=
又∵点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,
∴点M的轨迹在以A为球心以1半径的球面上
则点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比为:
•
•π:(
-
•
•π)=π:(64-π)
故答案为:
则棱锥A-BCD的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 32 |
| 3 |
又∵点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,
∴点M的轨迹在以A为球心以1半径的球面上
则点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比为:
| 1 |
| 8 |
| 4 |
| 3 |
| 32 |
| 3 |
| 1 |
| 8 |
| 4 |
| 3 |
故答案为:
| π |
| 64-π |
点评:本题考查的知识点是棱锥的体积及球的体积,其中判断出M的轨迹在以A为球心以1半径的球面上是解答本题的关键.

练习册系列答案
相关题目
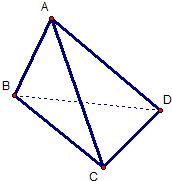 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=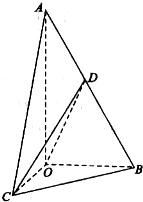 如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,
如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4, 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC. 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,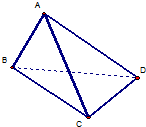 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=