Question

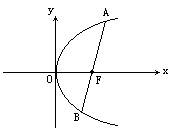
（08年长宁区质量抽测理） 在平面直角坐标系中，过定点作直线与抛物线相交于两点，如图，设动点、。

（1）求证：为定值；

（2）若点是点关于坐标原点的对称点，求面积的最小值；

（3）是否存在平行于轴的定直线，使得被以为直径的圆截得的弦长恒为定值？若存在，求出的方程；若不存在，请说明理由。

 

Answer 1

解析：（1）当直线垂直于轴时，，因此（定值）；

当直线不垂直于轴时，设直线的方程为：，

由得

因此有为定值。

（2）。

当直线垂直于轴时，；

当直线不垂直于轴时，由（1）知  因此，

。

综上，面积的最小值为。

（3）设存在直线满足条件。中点，

，因此以为直径的圆的半径，

中点到直线的距离，

所截弦长为：

，

当时，弦长=为定值。这时直线的方程为。