题目内容
一个工人看管三台机床,在一小时内,这三台机床需要工人照管的概率分别0.9、0.8、0.7,则没有一台机床需要工作照管的概率为 ( )
| A.0.006 | B.0.018 | C.0.06 | D.0.014 |
A
解析试题分析:由题意可得这3台机床不需要工人照管的概率分别为0.1、0.2、0.3,由此求得没有一台机床需要工人照管的概率为 0.1×0.2×0.3,运算求得结果。解:∵这三台机床需要工人照管的概率分别0.9、0.8、0.7,故这3台机床不需要工人照管的概率分别为0.1、0.2、0.3,∴没有一台机床需要工人照管的概率为 0.1×0.2×0.3=0.006,故选A.
考点:相互独立事件的概率
点评:本题主要考查相互独立事件的概率,事件与它的对立事件概率间的关系,得到这3台机床不需要工人照管的概率分别为0.1、0.2、0.3,是解题的关键,属于中档题

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
在区域D: 内随机取一个点,则此点到点A(1,2)的距离大于2的概率是( )
内随机取一个点,则此点到点A(1,2)的距离大于2的概率是( )
A. | B. | C. | D. |
甲乙两人玩猜数字游戏,先由甲在心中任想一个数字,记为 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,且
,且 。若
。若 ,则称甲乙“心有灵犀”。现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 ( )
,则称甲乙“心有灵犀”。现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 ( )
A. | B. | C. | D. |
在平面区域 内任意取一点
内任意取一点 内的概率是( )
内的概率是( )
A. | B. | C. | D. |
设函数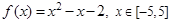 .若从区间
.若从区间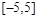 内随机选取一个实数
内随机选取一个实数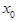 ,则所选取的实数
,则所选取的实数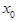 满足
满足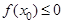 的概率为( )
的概率为( )
A.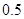 | B.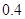 | C.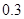 | D.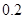 |





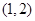 内随机取个实数
内随机取个实数 ,则直线
,则直线 ,直线
,直线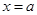 与
与 轴围成的面积大于
轴围成的面积大于 的概率是( )
的概率是( )



 的二项展开式中任取
的二项展开式中任取 项,
项, 表示取出的
表示取出的 项系数为奇数的概率. 若用随机变量
项系数为奇数的概率. 若用随机变量 表示取出的
表示取出的 ( )
( )



 满足约束条件
满足约束条件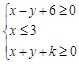 ,且
,且 的最小值为6.若实数
的最小值为6.若实数 则点
则点 落在上述区域内的概率为( )
落在上述区域内的概率为( )


