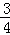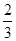题目内容
甲乙两人玩猜数字游戏,先由甲在心中任想一个数字,记为 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,且
,且 。若
。若 ,则称甲乙“心有灵犀”。现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 ( )
,则称甲乙“心有灵犀”。现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 ( )
A. | B. | C. | D. |
B
解析试题分析:根据题意,由于 ,那么可知满足题意的(a,b)共有16种,那么对于
,那么可知满足题意的(a,b)共有16种,那么对于 则可知a=b=1,a=b=2;a=b=3;a=b=4,a=1,b=2;a=2,b=3,a=3,b=4;反之也成立共有6+4=10种,则结合古典概型概率可知结论为
则可知a=b=1,a=b=2;a=b=3;a=b=4,a=1,b=2;a=2,b=3,a=3,b=4;反之也成立共有6+4=10种,则结合古典概型概率可知结论为 ,故答案为B.
,故答案为B.
考点:古典概型
点评:主要是考查了古典概型概率的计算,属于基础题。

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
一个工人看管三台机床,在一小时内,这三台机床需要工人照管的概率分别0.9、0.8、0.7,则没有一台机床需要工作照管的概率为 ( )
| A.0.006 | B.0.018 | C.0.06 | D.0.014 |
如果随机变量ξ~N(0,σ2),且P(-2<ξ≤0)="0.4" ,则P(ξ>2)等于:
| A.0.1 | B.0.2 | C.0.3 | D.0.4 |
 中,
中, ,若在菱形
,若在菱形 的概率是( )
的概率是( )



 B.
B.  C.
C.  D.
D. 
 的分布列如下:
的分布列如下:

 ( )
( )