题目内容
袋中有8个大小相同的小球,其中1个黑球,3个白球,4个红球.
(I)若从袋中一次摸出2个小球,求恰为异色球的概率;
(II)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,记此时红球的个数为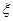 ,求
,求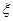 的分布列及数学期望E
的分布列及数学期望E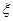 .
.
(I)若从袋中一次摸出2个小球,求恰为异色球的概率;
(II)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,记此时红球的个数为
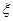 ,求
,求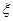 的分布列及数学期望E
的分布列及数学期望E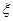 .
.(Ⅰ)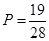 ;(Ⅱ)分布列为:
;(Ⅱ)分布列为:
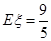 .
.
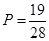 ;(Ⅱ)分布列为:
;(Ⅱ)分布列为: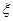 | 1 | 2 | 3 |
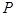 | 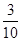 | 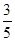 | 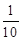 |
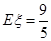 .
.试题分析:(Ⅰ)若从袋中一次摸出2个小球,求恰为异色球的概率,这显然是一个古典概型,有古典概型的概率求法,先求出总的基本事件数,从8个球中摸出2个小球的种数为
 ,再求出符合条件的基本事件数,摸出的2个小球为异色球的种数为
,再求出符合条件的基本事件数,摸出的2个小球为异色球的种数为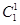
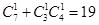 ,从而求出概率
,从而求出概率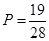 ;(Ⅱ)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,此时有三种:一种是有1个红球,1个黑球,1个白球,二种是有2个红球,1个其它颜色球,三种是所摸得的3小球均为红球,分别求出它们的概率,得分布列,从而求出期望.
;(Ⅱ)若从袋中一次摸出3个小球,且3个球中,黑球与白球的个数都没有超过红球的个数,此时有三种:一种是有1个红球,1个黑球,1个白球,二种是有2个红球,1个其它颜色球,三种是所摸得的3小球均为红球,分别求出它们的概率,得分布列,从而求出期望.试题解析:(Ⅰ)摸出的2个小球为异色球的种数为
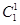
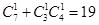 2分
2分从8个球中摸出2个小球的种数为
 3分
3分故所求概率为
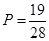 6分
6分(Ⅱ)符合条件的摸法包括以下三种:
一种是有1个红球,1个黑球,1个白球,
共有
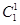
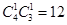 种 7分
种 7分一种是有2个红球,1个其它颜色球,
共有
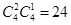 种, 8分
种, 8分一种是所摸得的3小球均为红球,共有
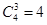 种不同摸法,
种不同摸法,故符合条件的不同摸法共有
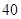 种. 10分
种. 10分由题意知,随机变量
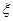 的取值为
的取值为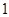 ,
,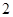 ,
,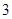 .其分布列为:
.其分布列为: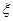 | 1 | 2 | 3 |
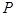 | 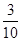 | 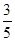 | 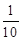 |
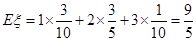 12分
12分
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
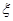 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出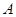 和获得等级不是
和获得等级不是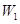 、
、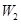 、
、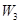 ,物理、化学、生物获得等级不是
,物理、化学、生物获得等级不是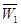 、
、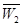 、
、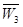 .
.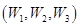 );
);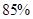 ,并说明理由.
,并说明理由.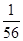 ;
;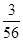 ;
;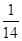 ;
;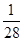 .
. 随机分成两组,使得每组至少有一个数,则两组中各数之和相等的概率是 ( )
随机分成两组,使得每组至少有一个数,则两组中各数之和相等的概率是 ( )


