题目内容
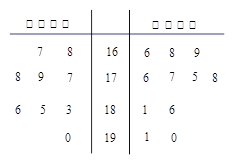
省少年篮球队要从甲、乙两所体校选拔队员。现将这两所体校共20名学生的身高绘制成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.
(Ⅰ)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随机选2人,那么至少有一人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中随机选3名队员,用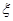 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出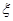 的分布列和数学期望.
的分布列和数学期望.

(Ⅰ)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随机选2人,那么至少有一人是“高个子”的概率是多少?
(Ⅱ)若从所有“高个子”中随机选3名队员,用
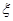 表示乙校中选出的“高个子”人数,试求出
表示乙校中选出的“高个子”人数,试求出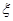 的分布列和数学期望.
的分布列和数学期望.(Ⅰ)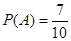 ;
;
(Ⅱ)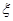 的分布列如下:
的分布列如下:
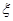 的期望为:
的期望为: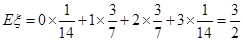 .
.
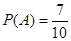 ;
;(Ⅱ)
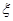 的分布列如下:
的分布列如下: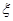 | 0 | 1 | 2 | 3 |
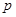 | 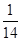 | 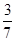 | 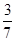 | 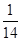 |
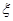 的期望为:
的期望为: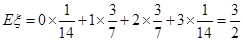 .
.试题分析:(Ⅰ)根据茎叶图可知这20名学生中有“高个子”8人,“非高个子”12人,因为采用分层抽样的方法从中抽取5人,故抽取比例为
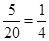 .根据这个比例可以求“高个子”和“非高个子”所抽取的人数.然后用古典概型公式可求出所要求的概率.
.根据这个比例可以求“高个子”和“非高个子”所抽取的人数.然后用古典概型公式可求出所要求的概率.(Ⅱ)据题意可知,这是一个超几何分布. 从乙校中选出“高个子”的人数
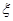 的所有可能为0,1,2,3.
的所有可能为0,1,2,3.由超几何分布公式可得:
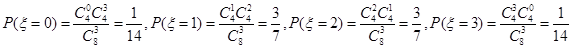
进而可得
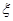 的分布列及期望.
的分布列及期望.试题解析:(Ⅰ)根据茎叶图可知这20名学生中有“高个子”8人,“非高个子”12人,用分层抽样的方法从中抽取5人,则应从“高个子”中抽取
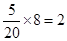 人,从“非高个子”中抽取
人,从“非高个子”中抽取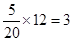 人。
人。用
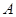 表示“至少有一名‘高个子’被选中”,则它的对立事件
表示“至少有一名‘高个子’被选中”,则它的对立事件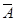 表示“没有一名‘高个子’被选中”,所以
表示“没有一名‘高个子’被选中”,所以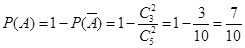 .
.(Ⅱ)依题意知,从乙校中选出“高个子”的人数
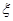 的所有可能值为0,1,2,3.
的所有可能值为0,1,2,3.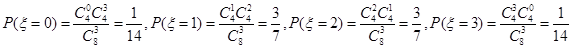
因此,
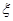 的分布列如下:
的分布列如下: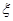 | 0 | 1 | 2 | 3 |
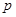 | 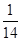 | 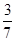 | 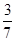 | 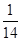 |
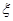 的期望为:
的期望为: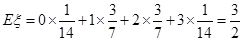 .
.
练习册系列答案
相关题目
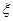 ,求
,求 店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4
店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4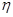 表示经销一辆该品牌汽车的利润.
表示经销一辆该品牌汽车的利润.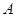 :“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率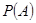 ;
;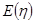 .
. 个同类产品(其中
个同类产品(其中 个是正品,
个是正品, 个是次品)中任意抽取
个是次品)中任意抽取 个的必然事件是( )
个的必然事件是( ) 个是次品
个是次品 中,任取两条棱,则这两条棱异面的概率是 .
中,任取两条棱,则这两条棱异面的概率是 .



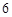 次,他们命中的环数如下表:
次,他们命中的环数如下表: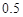 的概率.
的概率.