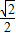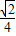题目内容
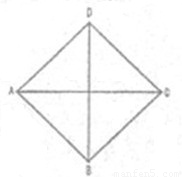
已知ABCD是空间四边形，AB=AD，CB=CD．E为BD的中点．求证：BD⊥平面ACE．分析：由条件利用等腰三角形的性质可得AE⊥BD，CE⊥BD．再利用直线和平面垂直的判定定理证得BD⊥平面ACE．
解答：解：∵已知ABCD是空间四边形，AB=AD，CB=CD，故△ABD和△CBD都是等腰三角形，
再由E为底边BD的中点，可得AE⊥BD，CE⊥BD．
而CE∩AE=E，故有BD⊥平面ACE．
解：∵已知ABCD是空间四边形，AB=AD，CB=CD，故△ABD和△CBD都是等腰三角形，再由E为底边BD的中点，可得AE⊥BD，CE⊥BD．
而CE∩AE=E，故有BD⊥平面ACE．
点评：本题主要考查等腰三角形的性质，直线和平面垂直的判定定理的应用，属于中档题．
练习册系列答案
相关题目
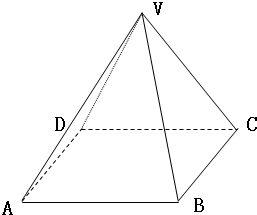如图，以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz，其中Ox∥BC，Oy∥AB；已知VA=kAB，点E是VC的中点，底面正方形ABCD边长为2a，高为h．
我们将底面是正方形，侧棱长都相等的棱锥称为正四棱锥．已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同，且如图所示，视图中四边形ABCD是边长为1的正方形，则该几何体的体积为（ ）
.
.
