题目内容
向量
=(2，0)，
=(2+2cosθ，2
+2sinθ)，则向量
与向量
夹角的范围是
| OA |
| OB |
| 3 |
| OA |
| OB |
[
，
]
| π |
| 6 |
| π |
| 2 |
[
，
]
．| π |
| 6 |
| π |
| 2 |
分析：确定
=(2+2cosθ，2
+2sinθ)表示以(2，2
)为圆心，2为半径的圆，利用直线与圆相切，确定直线的倾斜角，从而可求向量
与向量
夹角．
| OB |
| 3 |
| 3 |
| OA |
| OB |
解答：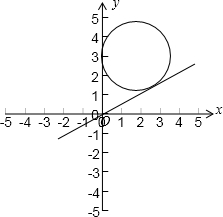
解：∵
=(2+2cosθ，2
+2sinθ)表示以(2，2
)为圆心，2为半径的圆
当斜率存在时，设过原点的直线方程为y=kx，则直线与圆相切时，
=2，∴k=
∵
=(2，0)
∴向量
与向量
夹角为
当斜率存在时，向量
与向量
夹角为
∴向量
与向量
夹角的范围是[
，
]
故答案为：[
，
]
解：∵| OB |
| 3 |
| 3 |
当斜率存在时，设过原点的直线方程为y=kx，则直线与圆相切时，
|-2k+2
| ||
|
| ||
| 3 |
∵
| OA |
∴向量
| OA |
| OB |
| π |
| 6 |
当斜率存在时，向量
| OA |
| OB |
| π |
| 2 |
∴向量
| OA |
| OB |
| π |
| 6 |
| π |
| 2 |
故答案为：[
| π |
| 6 |
| π |
| 2 |
点评：本题考查向量的夹角，考查数形结合的数学思想，将问题转化为直线与圆相切是关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目