题目内容
(本小题满分12分)
已知函数 在
在 上是增函数,在
上是增函数,在 上是减函数.
上是减函数.
(1)求函数 的解析式;
的解析式;
(2)若 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在实数 ,使得方程
,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出
上恰有两个相异实数根,若存在,求出 的范围,若不存在说明理由.
的范围,若不存在说明理由.
(1)
(2)
(3)
解析试题分析: ⑴
依题意得 ,所以
,所以 ,
,
从而 . ……4分
. ……4分
⑵ ,
,
令 ,得
,得 或
或 (舍去),
(舍去),
因为 在
在 递减,在
递减,在 递增,且
递增,且 ,
,
所以 ………8分
………8分
⑶设 ,
,
即 ,
, .
.
又 ,
,
令 ,得
,得 ;令
;令 ,得
,得 .
.
所以函数 的增区间为
的增区间为 ,减区间为
,减区间为 .
.
要使方程有两个相异实根,则有 ,
,
解得 . ……12分
. ……12分
考点:本小题主要考查利用导数求函数的单调区间,利用导数判断函数的单调性,解决有关方程的综合问题.
点评:纵观历年高考试题,利用导数讨论函数单调区间是函数考查的主要形式,是高考热点,是解答题中的必考题目,在复习中必须加强研究,进行专题训练,熟练掌握利用导数判断函数单调区间的方法,总结函数单调性应用的题型、解法,并通过加大训练强度提高解题能力.

练习册系列答案
相关题目
 在
在 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围.
的取值范围. 是函数
是函数 的一个极值点,且函数
的一个极值点,且函数 的图象在
的图象在 处的切线的斜率为2
处的切线的斜率为2 .
. ,其中
,其中 ,问:对于任意的
,问:对于任意的 ,方程
,方程
 在区间
在区间 上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.(9分)
上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.(9分) .
. 时,求
时,求 的极值;
的极值; 时,求
时,求 及
及 ,恒有
,恒有 成立,求
成立,求 的取值范围
的取值范围 ,
, .
. 时,求函数
时,求函数 的极值点;
的极值点; 的单调区间上也是单调的,求
的单调区间上也是单调的,求 的取值范围;
的取值范围; 时,设
时,设 ,且
,且 是函数
是函数 的极值点,证明:
的极值点,证明: .
. x2+ex-xex.(1)求f(x)的单调区间;
x2+ex-xex.(1)求f(x)的单调区间; ,
, 为何值时,
为何值时, 在
在 上取得最大值;
上取得最大值; ,若
,若 是单调递增函数,求
是单调递增函数,求 的取值范围.
的取值范围. ,
, =
=  (
(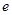 是自然对数的底)
是自然对数的底) 的取值范围;
的取值范围; >0,都有
>0,都有 ,求满足条件的最大整数
,求满足条件的最大整数 ,
, .
.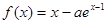 .
. 的单调区间;
的单调区间; 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.