题目内容
若直线y=k(x+1)与圆x2+y2-2x=0相切,则k= .
【答案】分析:把圆的方程化为标准式,求出圆心坐标和半径,利用切线的性质:圆心到切线的距离等于半径,列方程求k.
解答:解:圆x2+y2-2x=0 即 (x-1)2+y2=1,圆心(1,0),半径为1,直线y=k(x+1)即 kx-y+k=0,
由圆心到直线的距离等于半径得 1= 得 k=2,
得 k=2,
故答案为:2.
点评:本题考查圆的标准方程形式,点到直线的距离公式的应用,直线和圆的位置关系.
解答:解:圆x2+y2-2x=0 即 (x-1)2+y2=1,圆心(1,0),半径为1,直线y=k(x+1)即 kx-y+k=0,
由圆心到直线的距离等于半径得 1=
 得 k=2,
得 k=2,故答案为:2.
点评:本题考查圆的标准方程形式,点到直线的距离公式的应用,直线和圆的位置关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
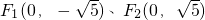 ,动点P满足条件:
,动点P满足条件: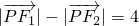 ,设点P的轨迹是曲线E,O为坐标原点.
,设点P的轨迹是曲线E,O为坐标原点.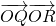 的取值范围;
的取值范围;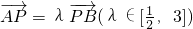 ,记xA、xB分别为A、B两点的横坐标,求|xA•xB|的最小值.
,记xA、xB分别为A、B两点的横坐标,求|xA•xB|的最小值.