题目内容

椭圆
x2
3
+y2=1被直线x-y+1=0所截得的弦长|AB|=（　　）
分析：直线方程与椭圆方程联立，求出A，B坐标，利用两点间的距离公式可得结论．
解答：解：由
x-y+1=0
x2
3
+y2=1
，消y可得x（2x+3）=0，∴x=0或x=-
3
2

x=0时，y=1；x=-
3
2
时，y=-
1
2
，
∴|AB|=
(0+
3
2
)2+(1+
1
2
)2
=
3
2
2

故选B．
点评：本题考查直线与椭圆的位置关系，考查弦长的计算，求出A，B的坐标是关键．
练习册系列答案
相关题目
在平面直角坐标系xOy中，设P（x，y）是椭圆
x2
3
+y2=1上的一个动点，则S=x+y的最大值是（　　）
A、1B、2C、3D、4
直线l与椭圆
x2
3
+y2=1交于不同的两点P1，P2，线段P1P2的中点为P，设直线l的斜率为k1（k1≠0），直线OP的斜率为k2（O点为坐标原点），则k1•k2的值为（　　）
已知直线l：y=kx+m与椭圆
x2
3
+y2=1交于A、B两点，坐标原点O到直线l的距离为
3
2
，设弦长|AB|=f（k）
（1）求f（k）个关于实数k的表达式；
（2）若不等式|x-p|+|x-1|≥f（k）对k∈R，x∈R恒成立，求实数p的取值范围．
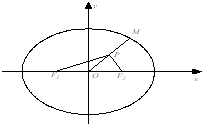如图，M为椭圆
x2
3
+y2=1上任意一点，P为线段OM的中点，求
PF1
•
PF2
的最小值
-
7
4
-
7
4
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网