Question

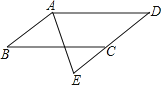
【题目】如图，三棱柱中，侧面底面，，，且，点，，分别为，，的中点．

（Ⅰ）求证：平面．

（Ⅱ）求证：平面．

（Ⅲ）写出四棱锥的体积．（只写出结论，不需要说明理由）

Answer 1

【答案】(1)见解析;(2)见解析;(3).

【解析】试题分析：（1）由三线合一得A1D⊥AC，再利用面面垂直的性质得出A1D⊥平面ABC；

（2）取B1C1的中点为G，连结FG，GB，则可证明四边形FGBE为平行四边形，从而EF∥BG，于是EF∥平面BB1C1C；

（3）过A1作A1M⊥CC1，垂足为M，则可证明A1M⊥平面BCC1B1．于是A1M为四棱锥A1﹣BB1C1C的高，底面为矩形，代入体积公式计算即可．

（1）证明：∵，

∴是等边三角形，

在等边中，

是边的中点，

∴，

又∵侧面底面，

侧面底面．

侧面，

∴平面．

（2）取中点，连接，，

∵，，分别是，，中点，

∴，

∴四边形是平行四边形，

∴．

又∵平面，

平面，

∴平面，

（3）．