题目内容
【题目】如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是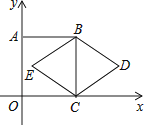
【答案】(2+ ![]() ,1)
,1)
【解析】解:过点D作DG⊥BC于点G,
∵四边形BDCE是菱形,
∴BD=CD.
∵BC=2,∠D=60°,
∴△BCD是等边三角形,
∴BD=BC=CD=2,
∴CG=1,GD=CDsin60°=2× ![]() =
= ![]() ,
,
∴D(2+ ![]() ,1).
,1).
故答案为:(2+ ![]() ,1).
,1).
过点D作DG⊥BC于点G,根据四边形BDCE是菱形可知BD=CD,再由BC=2,∠D=60°可得出△BCD是等边三角形,由锐角三角函数的定义求出GD及CG的长即可得出结论.本题考查的是正方形的性质,根据题意作出辅助线,利用菱形的性质判断出△BCD是等边三角形是解答此题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目