题目内容
已知函数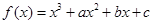 在
在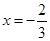 与
与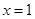 时都取得极值
时都取得极值
(1)求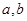 的值与函数
的值与函数 的单调区间
的单调区间
(2)若对 ,不等式
,不等式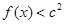 恒成立,求
恒成立,求 的取值范围
的取值范围
(1) 递增区间是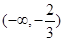 与
与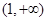 ,递减区间是
,递减区间是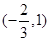 ;(2)
;(2)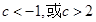 .
.
解析试题分析:(1)求出f′(x),因为函数在x=-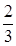
与x=1时都取得极值,所以得到f′(-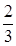 )=0且f′(1)=0联立解得a与b的值,然后把a、b的值代入求得f(x)及f′(x),然后讨论导函数的正负得到函数的增减区间;
)=0且f′(1)=0联立解得a与b的值,然后把a、b的值代入求得f(x)及f′(x),然后讨论导函数的正负得到函数的增减区间;
(2)根据(1)函数的单调性,由于x∈[-1,2]恒成立求出函数的最大值值为f(2),代入求出最大值,然后令f(2)<c2列出不等式,求出c的范围即可..
试题解析:解:(1) 1分;
1分;
由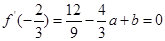 ,
,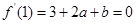 得
得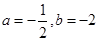 3分;
3分;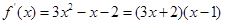 ,函数
,函数 的单调区间如下表:
的单调区间如下表:
所以函数 
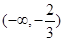
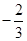
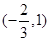
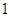
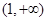
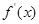
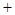

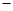

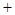

极大值 ¯ 极小值  的递增区间是
的递增区间是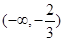 与
与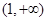 ,递减区间是
,递减区间是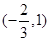 ; 6分;
; 6分;
(2)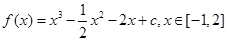 ,当
,当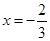 时,
时,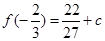
为极大值,而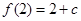 ,则
,则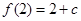 为最大值, 9分;
为最大值, 9分;
要使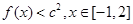 恒成立,则只需要
恒成立,则只需要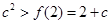 , 10分;
, 10分;
得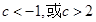 12分;
12分;
考点:1.利用导数研究函数的极值;2.函数恒成立问题;3.利用导数研究函数的单调性..

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
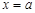 和
和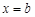 是函数
是函数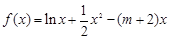 的两个极值点,其中
的两个极值点,其中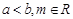 .
.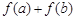 的取值范围;
的取值范围;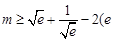 为自然对数的底数),求
为自然对数的底数),求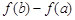 的最大值.
的最大值.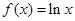 ,
,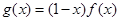
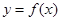 在点(1,0)处的切线方程;
在点(1,0)处的切线方程;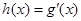 及
及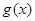 在区间
在区间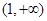 上的单调性;
上的单调性;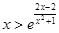 在
在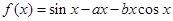
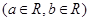 .
.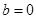 ,讨论函数
,讨论函数 在区间
在区间 上的单调性;
上的单调性;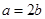 且对任意的
且对任意的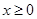 ,都有
,都有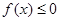 恒成立,求实数
恒成立,求实数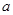 的取值范围.
的取值范围. (万元),已知产品单价P(万元)与产品件数x满足:
(万元),已知产品单价P(万元)与产品件数x满足: ,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?
,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?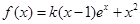 .
. ,求函数
,求函数 在点(1,1)处的切线方程;
在点(1,1)处的切线方程;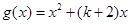 的图象恒在
的图象恒在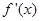 图象的上方,求k的取值范围;
图象的上方,求k的取值范围; 函数
函数 在
在 上是单调递减函数,
上是单调递减函数, 方程
方程 无实根,若“
无实根,若“ 或
或 ”为真,“
”为真,“ 的取值范围。
的取值范围。 ,其中
,其中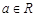 .
.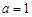 ,求函数
,求函数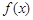 的极值点;
的极值点;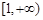 内单调递增,求实数
内单调递增,求实数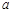 的取值范围.
的取值范围.