题目内容
设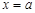 和
和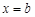 是函数
是函数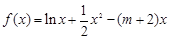 的两个极值点,其中
的两个极值点,其中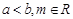 .
.
(1)求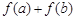 的取值范围;
的取值范围;
(2)若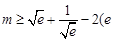 为自然对数的底数),求
为自然对数的底数),求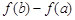 的最大值.
的最大值.
(1)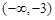 ;(2)
;(2)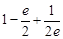
解析试题分析:(1)先求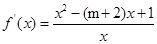 ,由已知条件得,方程
,由已知条件得,方程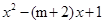 =0有两个不等的正根
=0有两个不等的正根 ,则有
,则有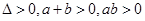 ,解得
,解得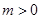 ,结合韦达定理将
,结合韦达定理将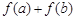 变形为关于变量
变形为关于变量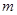 的函数表达式,
的函数表达式,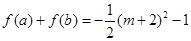 ,进而求值域得
,进而求值域得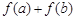 的取值范围;(2)将
的取值范围;(2)将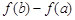 变形为
变形为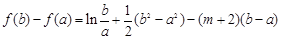 ,为了减少参数,将
,为了减少参数,将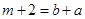 代入得,
代入得,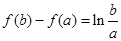
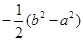 ,为了便于求值域,利用
,为了便于求值域,利用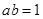 ,继续变形为
,继续变形为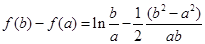
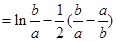 ,设
,设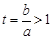 ,通过还原,将
,通过还原,将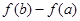 表示为变量
表示为变量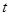 的函数,进而求值域即可.
的函数,进而求值域即可.
(1)函数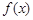 的定义域为
的定义域为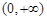 ,
,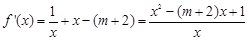 .
.
依题意,方程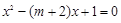 有两个不等的正根
有两个不等的正根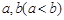 ,
,
故有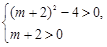 ,解得
,解得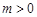 ,且
,且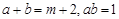 ,
,
所以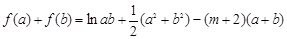 ,
,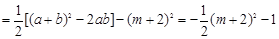 ,
,
又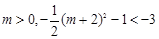 ,所以
,所以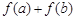 的取值范围是
的取值范围是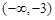 . 6分
. 6分
(2)由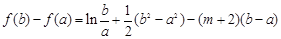 ,
,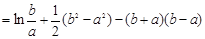
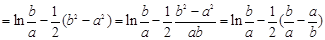
令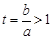 ,所以
,所以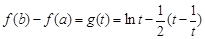 ,
,
又因为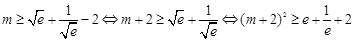 ,
,
所以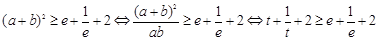 ,可化为
,可化为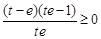 ,因为
,因为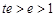 ,所以得
,所以得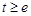 ,求
,求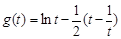 在
在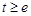 上最大值,
上最大值,
由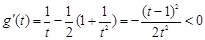 ,所以
,所以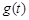 在
在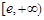 上递减,
上递减,
所以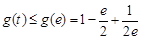 ,故
,故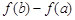 的最大值为
的最大值为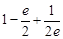 . 13分
. 13分
考点:1、利用导数求函数的极值和最值;1、利用导数判断函数的单调性.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
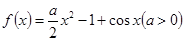 .
.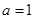 时,求函数
时,求函数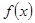 在
在 上的最大值和最小值;
上的最大值和最小值; 上为增函数,求正数
上为增函数,求正数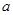 的取值范围.
的取值范围. 时,有g(x)≤0.
时,有g(x)≤0.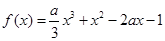 ,
,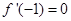 .
. 的单调区间;
的单调区间;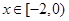 ,都有
,都有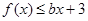 ,求
,求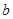 的取值范围.
的取值范围.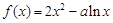 .
.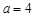 ,求函数
,求函数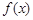 的极小值;
的极小值;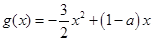 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量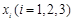 使得
使得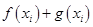 的值相等,若存在,请求出
的值相等,若存在,请求出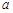 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由? 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.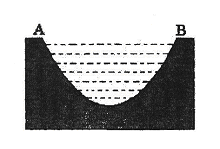
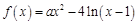 ,
,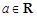 .
.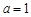 时,求
时,求 的单调区间;
的单调区间;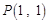 和函数
和函数 ,对任意
,对任意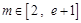 ,直线
,直线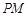 倾斜角都是钝角,求
倾斜角都是钝角,求 的取值范围.
的取值范围.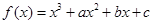 在
在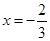 与
与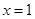 时都取得极值
时都取得极值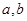 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式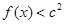 恒成立,求
恒成立,求 的取值范围
的取值范围