题目内容
数列{an}满足:an+1=3an-3an2,n=1,2,3,…。
(Ⅰ)若数列{an}为常数列,求a1的值;
(Ⅱ)若a1=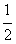 ,求证:
,求证: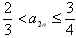 ;
;
(Ⅲ)在(Ⅱ)的条件下,求证:数列{a2n}单调递减。
(Ⅰ)若数列{an}为常数列,求a1的值;
(Ⅱ)若a1=
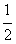 ,求证:
,求证: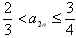 ;
; (Ⅲ)在(Ⅱ)的条件下,求证:数列{a2n}单调递减。
(Ⅰ)解:因为数列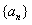 为常数列,
为常数列,
所以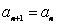 ,
,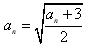 ,
,
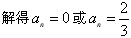 ,
,
由n的任意性知,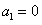 或
或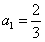 。
。
(Ⅱ)证明:用数学归纳法证明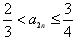 ,
,
①当n=1时,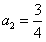 ,符合上式;
,符合上式;
②假设当n=k(k≥1)时,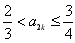 ,
,
因为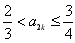 , 所以
, 所以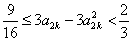 ,即
,即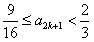 ,
,
从而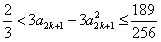 ,即
,即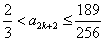 ,
,
因为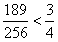 ,
,
所以,当n=k+1时,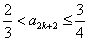 成立,
成立,
由①,②知,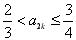 。
。
(Ⅲ)证明:因为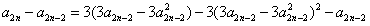
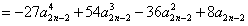 (n≥2),
(n≥2),
所以只要证明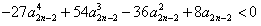 ,
,
由(Ⅱ)知,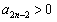 ,
,
所以只要证明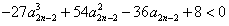 ,
,
即证明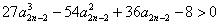 ,
,
令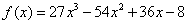 ,
,
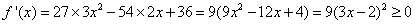 ,
,
所以函数f(x)在R上单调递增;
因为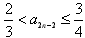 ,
,
所以,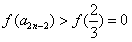 ,即
,即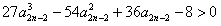 成立,
成立,
故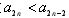 ,所以数列
,所以数列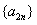 单调递减。
单调递减。
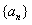 为常数列,
为常数列,所以
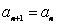 ,
,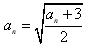 ,
,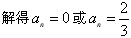 ,
,由n的任意性知,
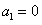 或
或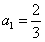 。
。(Ⅱ)证明:用数学归纳法证明
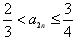 ,
,①当n=1时,
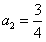 ,符合上式;
,符合上式;②假设当n=k(k≥1)时,
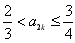 ,
, 因为
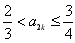 , 所以
, 所以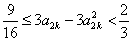 ,即
,即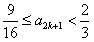 ,
,从而
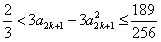 ,即
,即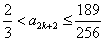 ,
,因为
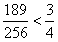 ,
,所以,当n=k+1时,
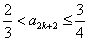 成立,
成立,由①,②知,
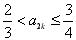 。
。 (Ⅲ)证明:因为
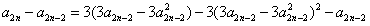
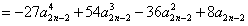 (n≥2),
(n≥2),所以只要证明
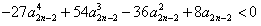 ,
,由(Ⅱ)知,
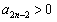 ,
,所以只要证明
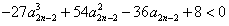 ,
,即证明
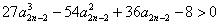 ,
,令
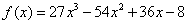 ,
,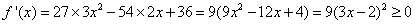 ,
,所以函数f(x)在R上单调递增;
因为
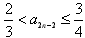 ,
,所以,
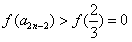 ,即
,即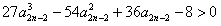 成立,
成立,故
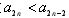 ,所以数列
,所以数列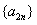 单调递减。
单调递减。
练习册系列答案
相关题目