题目内容
如图,四棱锥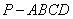 中,底面
中,底面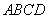 为矩形,
为矩形,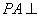 底面
底面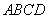 ,
,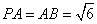 ,点
,点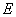 是棱
是棱 的中点.
的中点.
(Ⅰ)求证:直线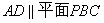 ;
;
(Ⅱ) 求直线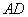 与平面
与平面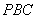 的距离;
的距离;
(Ⅲ)若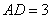 ,求二面角
,求二面角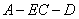 的平面角的余弦值.
的平面角的余弦值.
(1)在矩形ABCD中,AD∥BC,又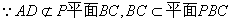
 AD∥平面PBC
AD∥平面PBC
(2)如右图,以A为坐标原点,射线 AB、AD、AP分别为x轴、y轴、z轴正半轴,建立空间直角坐标系A-xyz.设D(0,a,0),则B (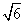 ,0,0),C(
,0,0),C(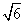 ,a,0),P(0,0,
,a,0),P(0,0,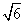 ),E(
),E(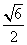 ,0,
,0,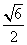 ).
).
因此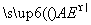 =(
=(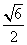 ,0,
,0,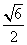 ),
),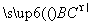 =(0,a,0),
=(0,a,0),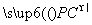 =(
=(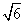 ,0,-
,0,-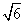 ).
).
则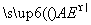 ·
·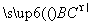 =0,
=0,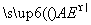 ·
·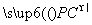 =0,所以AE⊥平面PBC.又由AD∥BC知AD∥平面PBC,
=0,所以AE⊥平面PBC.又由AD∥BC知AD∥平面PBC,
故直线 AD与平面PBC的距离为点A到平面PBC的距离,即为|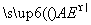 |=
|=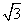 .
.
(3)因为|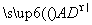 |=
|=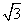 ,则D(0,
,则D(0,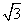 ,0),C(
,0),C(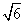 ,
,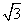 ,0).
,0).
设平面AEC的法向量n1=(x1,y1, z1),则n1· =0,n1·
=0,n1·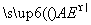 =0.
=0.
又 =(
=(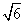 ,
,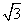 ,0),
,0),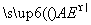 =(
=(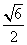 ,0,
,0,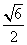 ),故
),故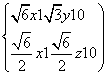
所以y1=- x1,z1=-x1.可取x1=-
x1,z1=-x1.可取x1=- ,则n1=(-
,则n1=(- ,2,
,2, ).
).
设平面DEC的法向量n2=(x2,y2,z2),则n2·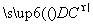 =0,n2·
=0,n2·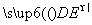 =0,
=0,
又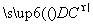 =(
=(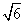 ,0,0),
,0,0),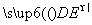 =(
=(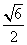 ,-
,-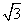 ,
,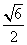 ),故
),故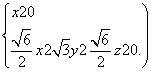
所以x2=0,z2= y2,可取y2=1,则n2=(0,1,
y2,可取y2=1,则n2=(0,1, ).
).
故cos〈n1,n2〉=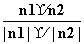 =
=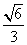 .
.

练习册系列答案
相关题目
 与圆
与圆 外切,而与圆
外切,而与圆 内切,那么动圆的圆心
内切,那么动圆的圆心 的离心率为 ;若抛物线
的离心率为 ;若抛物线 的焦点恰好为该双曲线的右焦点,则
的焦点恰好为该双曲线的右焦点,则 的值为 .
的值为 . ,则以
,则以 为邻边的平行四边形的面积为( ).
为邻边的平行四边形的面积为( ). C.4 D.
C.4 D.
 的焦点为
的焦点为 ,经过
,经过 两点,则以AB为直径的圆在
两点,则以AB为直径的圆在 轴上所截得的弦长的最小值是 。
轴上所截得的弦长的最小值是 。 表示双曲线,那么实数
表示双曲线,那么实数 的取值范围是( ).
的取值范围是( ). B .
B . 或
或 D .
D . 或
或 在点(1,
在点(1, )处的切线与直线
)处的切线与直线 平行,则
平行,则 ( )
( ) C.
C.  D.
D. 
 且在
且在 轴、
轴、 轴截距相等的直线方程为
轴截距相等的直线方程为





