题目内容
7.设实数x,y满足$\left\{\begin{array}{l}{2x+y≤6}\\{x+2y≤6}\\{x≥0,y≥0}\end{array}\right.$,则Z=max{2x+y-1,x+2y+2}的取值范围是[-1,5].分析 作出不等式组对应的平面区域,利用作差法求出z的表达式,然后根据平移,根据数形结合即可得到结论.
解答 解:作出不等式组对应的平面区域如图:
2x+y-1-(x+2y+2)=x-y-3,
即z=max{2x+y-1,x+2y+2}=$\left\{\begin{array}{l}{2x+y-1,x-y-3≥0\\;}\\{x+2y+2,x-y-3<0}\end{array}\right.$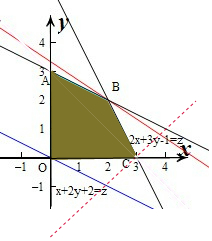
其中直线x-y-3=0过C点.
在直线x-y-3=0的上方,平移直线z=2x+y-1(红线),当直线z=2x+y-1经过点B(2,2)时,
直线z=2x+y-1的截距最大,
此时z取得最大值为z=2×2+2-1=5.
可行域没有在直线x+y-3=0的下方的,平移直线z=x+2y+2,当直线z=2x+y-1经过点O(0,0)时,
直线z=2x+y-1的截距最小,
此时z取得最小值为z=-1.
即-1≤z≤5,
故答案为:[-1,5].
点评 本题主要考查线性规划的应用,根据z的几何意义确定对应的直线方程是截距本题的关键.难度较大.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
18.曲线f(x)=-x3+3x2在点(1,f(1))处的切线截圆x2+(y+1)2=4所得弦长为( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
19.△ABC的三边长分别为|AB|=7,|BC|=5,|CA|=6,则$\overrightarrow{AB}$•$\overrightarrow{BC}$ 的值为( )
| A. | 19 | B. | 14 | C. | -18 | D. | -19 |
16.已知函数f(x)=2x,等差数列{an}的公差为2.若f(a2+a4+a6+a8+a10)=4,则log2[f(a1)•f(a2)•f(a3)•…•f(a10)]=( )
| A. | 8 | B. | 4 | C. | -6 | D. | $\frac{1}{4}$ |
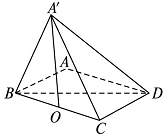 如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.
如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°.