Question

【题目】已知函数．

（1）求f（x）的定义域；

（2）当x∈（1，+∞），

①求证：f（x）在区间（1，+∞）上是减函数；

②求使关系式f（2+m）＞f（2m-1）成立的实数m的取值范围．

Answer 1

【答案】(1) （-∞，-1）∪（1，+∞）．(2) ①证明见解析； ②m＞3．

【解析】

（1）由＞0，得x＜-1或x＞1，答案可求；

（2）①设1＜x1＜x2，f（x1）-f（x2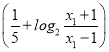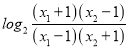）=（）==，判断正负得出结论；

②由①知函数f（x）在（1，+∞）上是减函数，由f（2+m）＞f（2m-1）得出m．

（1）由＞0，得x＜-1或x＞1，

即函数的定义域为（-∞，-1）∪（1，+∞）．

（2）①证明：设1＜x1＜x2，

f（x1）-f（x2）=-（）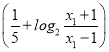

==，

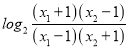因为1＜x1＜x2，所以x2-x1＞0，

所以x1x2-1+（x2-x1）＞x1x2-1-（x2-x1）＞0，

所以，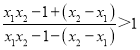

所以f（x）＞f（x），

故f（x）在（1，+∞）上是减函数．

②由（1）知函数f（x）在（1，+∞）上是减函数，

由f（2+m）＞f（2m-1），

得1＜2+m＜2m-1，得m＞3．