题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)如图,若斜率为k(k≠0)的直线l与x轴,椭圆C顺次交于P,Q,R(P点在椭圆左顶点的左侧)且∠RF1F2=∠PF1Q,求证:直线l过定点,并求出斜率k的取值范围.
考点:椭圆的简单性质
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:(Ⅰ)求出椭圆的焦点,由离心率可得b=c,再由直线和圆相切的条件d=r,可得b=1,进而得到a,即可求得椭圆方程;
(Ⅱ)设Q(x1,y1),R(x2,y2),F1(-1,0),由∠RF1F2=∠PF1Q,可得直线QF1和RF1关于x轴对称,运用直线的斜率公式,设直线PQ:y=kx+t,代入椭圆方程,运用判别式大于0,以及韦达定理,化简整理即可得到t=2k,进而得到直线l恒过定点(-2,0),由二次不等式解法即可得到k的范围.
(Ⅱ)设Q(x1,y1),R(x2,y2),F1(-1,0),由∠RF1F2=∠PF1Q,可得直线QF1和RF1关于x轴对称,运用直线的斜率公式,设直线PQ:y=kx+t,代入椭圆方程,运用判别式大于0,以及韦达定理,化简整理即可得到t=2k,进而得到直线l恒过定点(-2,0),由二次不等式解法即可得到k的范围.
解答:
(Ⅰ)解:椭圆的左,右焦点分别为F1(-c,0),F2(c,0),
椭圆的离心率为
,即有
=
,即a=
c,b=
=c,
以原点为圆心,椭圆的短半轴长为半径的圆方程为x2+y2=b2,
直线y=x+
与圆相切,则有
=1=b,
即有a=
,
则椭圆C的方程为
+y2=1;
(Ⅱ)证明:设Q(x1,y1),R(x2,y2),F1(-1,0),
由∠RF1F2=∠PF1Q,可得直线QF1和RF1关于x轴对称,
即有kQF1+kRF1=0,即
+
=0,
即有x1y2+y2+x2y1+y1=0,①
设直线PQ:y=kx+t,代入椭圆方程,可得
(1+2k2)x2+4ktx+2t2-2=0,
判别式△=16k2t2-4(1+2k2)(2t2-2)>0,
即为t2-2k2<1②
x1+x2=
,x1x2=
,③
y1=kx1+t,y2=kx2+t,
代入①可得,(k+t)(x1+x2)+2t+2kx1x2=0,
将③代入,化简可得t=2k,
则直线l的方程为y=kx+2k,即y=k(x+2).
即有直线l恒过定点(-2,0).
将t=2k代入②,可得2k2<1,
解得-
<k<0或0<k<
.
则直线l的斜率k的取值范围是(-
,0)∪(0,
).
椭圆的离心率为
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| 2 |
| a2-c2 |
以原点为圆心,椭圆的短半轴长为半径的圆方程为x2+y2=b2,
直线y=x+
| 2 |
|
| ||
|
即有a=
| 2 |
则椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)证明:设Q(x1,y1),R(x2,y2),F1(-1,0),
由∠RF1F2=∠PF1Q,可得直线QF1和RF1关于x轴对称,
即有kQF1+kRF1=0,即
| y1 |
| x1+1 |
| y2 |
| x2+1 |
即有x1y2+y2+x2y1+y1=0,①
设直线PQ:y=kx+t,代入椭圆方程,可得
(1+2k2)x2+4ktx+2t2-2=0,
判别式△=16k2t2-4(1+2k2)(2t2-2)>0,
即为t2-2k2<1②
x1+x2=
| -4kt |
| 1+2k2 |
| 2t2-2 |
| 1+2k2 |
y1=kx1+t,y2=kx2+t,
代入①可得,(k+t)(x1+x2)+2t+2kx1x2=0,
将③代入,化简可得t=2k,
则直线l的方程为y=kx+2k,即y=k(x+2).
即有直线l恒过定点(-2,0).
将t=2k代入②,可得2k2<1,
解得-
| ||
| 2 |
| ||
| 2 |
则直线l的斜率k的取值范围是(-
| ||
| 2 |
| ||
| 2 |
点评:本题考查椭圆的方程和性质,主要是离心率的运用,注意运用直线和圆相切的条件,联立直线方程和椭圆方程,运用韦达定理,考查化简整理的运算能力,属于中档题和易错题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
已知复数z=(1-sinθ)+icosθ(θ∈[
,π]),则|z|等于( )
| π |
| 2 |
A、cos
| ||||||
B、sin
| ||||||
C、
| ||||||
D、
|
 已知函数f(x)=Asin(ωx-
已知函数f(x)=Asin(ωx-| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
“φ=2kπ+
,k∈Z”是“函数f(x)=cos(2x+φ)的图象过原点”的( )
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
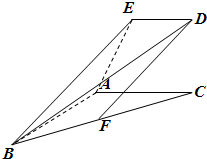 如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.
如图所示,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,AB=AC=AE=2ED=2a,F是BC的中点.