题目内容
等差数列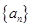 的前
的前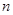 项和是
项和是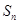 ,若
,若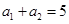 ,
,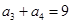 ,则
,则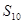 的值为( )
的值为( )
| A.55 | B.65 | C.60 | D.70 |
B
解析试题分析:根据已知条件,由于等差数列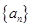 的前
的前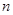 项和是
项和是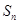 ,若
,若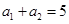 ,
,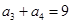 ,那么第二式减去第一式可知为4d=4,d=1,代入第一式中可知为2
,那么第二式减去第一式可知为4d=4,d=1,代入第一式中可知为2 ,那么可知
,那么可知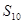 =10
=10 ,故答案为B.
,故答案为B.
考点:等差数列的通项公式和求和
点评:解决的关键是利用整体的思想先求解公差,然后再结合代入法得到首项,进而求解得到和,属于基础题。

练习册系列答案
相关题目
数列 的首项为3,
的首项为3, 为等差数列且
为等差数列且 ,若
,若 ,则
,则 ( )
( )
| A.0 | B.3 | C.8 | D.11 |
已知等差数列 中,
中, ,则
,则 的值是 ( )
的值是 ( )
| A.15 | B.30 | C.31 | D.64 |
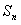 是等差数列
是等差数列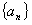 的前
的前 项和,若
项和,若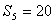 ,则
,则 ( )
( )
| A.15 | B.18 | C.9 | D.12 |
已知等差数列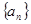 的公差为
的公差为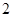 ,若
,若 成等比数列, 则
成等比数列, 则 ( )
( )
A.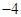 | B.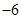 | C.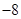 | D.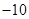 |
设等差数列 的前n项和为
的前n项和为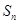 ,若
,若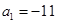 ,
, ,则当
,则当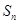 取最小值时,n等于( )
取最小值时,n等于( )
| A.6 | B.7 | C.8 | D.9 |
已知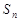 是等差数列
是等差数列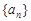 的前
的前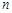 项和,若
项和,若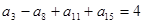 ,则
,则 的值是
的值是
| A.5 | B.8 | C.16 | D.20 |
已知 为等差数列,若
为等差数列,若 ,则
,则 的值为
的值为
A. | B. | C. | D. |