题目内容
已知等差数列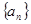 的公差为
的公差为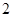 ,若
,若 成等比数列, 则
成等比数列, 则 ( )
( )
A.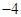 | B.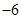 | C.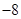 | D.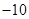 |
B
解析试题分析:由题意,因为 成等比数列,所以
成等比数列,所以 ,所以
,所以 ,
,
所以
考点:等比数列的性质 等差数列的通项公式
点评:本题以等差数列,等比数列为载体,综合考查等差数列和等比数列,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设等差数列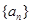 的前
的前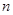 项和为
项和为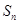 ,若
,若 ,
, ,则
,则 ( )
( )
| A.63 | B.45 | C.36 | D.27 |
如果等差数列 中,
中,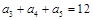 ,那么
,那么 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
等差数列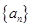 的前
的前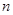 项和是
项和是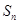 ,若
,若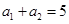 ,
,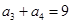 ,则
,则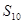 的值为( )
的值为( )
| A.55 | B.65 | C.60 | D.70 |
在等差数列中,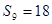 ,
, ,
,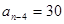 ,则
,则 的值为( )。
的值为( )。
| A.14 | B.15 | C.16 | D.75 |
在等差数列 中,已知
中,已知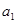 +
+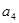 +
+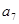 =39,
=39, +
+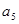 +
+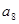 =33,则
=33,则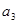 +
+ +
+ =( )
=( )
| A.30 | B.27 | C.24 | D.21 |
《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样的一道题目:把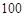 个面包分给
个面包分给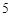 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的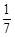 是较小的两份之和,则最小的
是较小的两份之和,则最小的 份为
份为
A.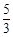 | B. | C.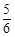 | D.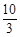 |
已知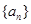 为等差数列,
为等差数列, ,则
,则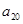 等于( )
等于( )
| A.10 | B.20 | C.40 | D.80 |
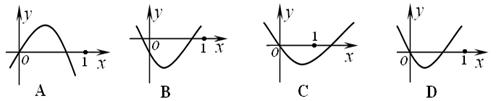
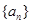 ,其前
,其前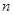 项和为
项和为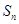 ,则点
,则点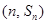 所在的抛物线可能为
所在的抛物线可能为