题目内容
【题目】设椭圆![]() 的离心率
的离心率![]() ,左顶点
,左顶点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若以
两点,若以![]() 为直径的圆经过坐标原点,证明:点
为直径的圆经过坐标原点,证明:点![]() 到直线
到直线![]() 的距离为定值;
的距离为定值;
(III)在(Ⅱ)的条件下,试求![]() 的面积
的面积![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)定值为
;(2)定值为![]() ;(3)
;(3)![]()
【解析】
试题(1)根据题目条件建立a,b,c的两个方程,可求得椭圆的标准方程;(2)以AB为直径的圆经过坐标原点,等价于OA⊥OB,再转换为x1x2+y1y2=0,结合A、B是直线与椭圆的公共点,可得原点到直线的距离为定值;(3)结合(2),将三角形的面积表示为直线斜率的函数关系式,利用二次函数的性质可求的面积的最小值.
试题解析:(1)由e=![]() ,得c=
,得c=![]() a,又b2=a2-c2,所以b=
a,又b2=a2-c2,所以b=![]() a,即a=2b.
a,即a=2b.
由左顶点M(-a,0)到直线![]() ,即bx+ay-ab=0的距离d=
,即bx+ay-ab=0的距离d=![]() ,
,
得![]() ,即
,即![]() ,
,
把a=2b代入上式,得![]() ,解得b=1.所以a=2b=2,c=
,解得b=1.所以a=2b=2,c=![]() .
.
所以椭圆C的方程为![]() . 3分
. 3分
(2)设A(x1,y1),B(x2,y2),
①当直线AB的斜率不存在时,则由椭圆的对称性,可知x1=x2,y1=-y2.
因为以AB为直径的圆经过坐标原点,故![]() =0,
=0,
即x1x2+y1y2=0,也就是![]() ,
,
又点A在椭圆C上,所以![]() ,
,
解得|x1|=|y1|=![]() .
.
此时点O到直线AB的距离d1=|x1|=![]() .
.
②当直线AB的斜率存在时,
设直线AB的方程为y=kx+m,
与椭圆方程联立有
消去y,得(1+4k2)x2+8kmx+4m2-4=0
所以![]()
因为以AB为直径的圆经过坐标原点O,所以OA⊥OB
于是![]() =x1x2+y1y2=0,
=x1x2+y1y2=0,
所以(1+k2)x1x2+km(x1+x2)+m2=0
所以![]()
整理得:5m2=4(k2+1)
所以点O到直线AB的距离d1=![]() .
.
综上所述,点O到直线AB的距离为定值![]() . 8分
. 8分
(3)设直线OA的斜率为k0.
当k0≠0时,
则OA的方程为y=k0x,OB的方程为![]() ,
,
联立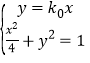 得
得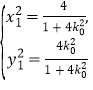 同理可求得
同理可求得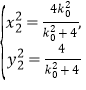
故△AOB的面积为S=![]() =2
=2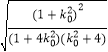 .
.
令1+![]() =t(t>1),
=t(t>1),
则S=2![]() =2
=2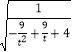 ,
,
令g(t)=![]() (t>1),所以4<g(t)≤
(t>1),所以4<g(t)≤![]() .所以
.所以![]() ≤S<1.
≤S<1.
当k0=0时,可求得S=1,
故![]() ≤S≤1,故S的最小值为
≤S≤1,故S的最小值为![]() . 13分
. 13分

【题目】“微信运动”是一个类似计步数据库的公众帐号,用户只需以运动手环或手机协处理器的运动教据为介,然后关注该公众号,就能看见自己与好友每日行走的步数,并在同一排行榜上得以体现,现随机选取朋友圈中的50人记录了他们某一天的走路步数,并将数据整理如下:

规定:人一天行走的步数超过8000步时被系统评定为“积极性”,否则为“懈怠性”.
(1)填写下面列联表(单位:人),并根据列联表判断是否有![]() 的把握认为“评定类型与性别有关”;
的把握认为“评定类型与性别有关”;

附:
|
|
|
|
|
|
|
|
|
|
|
|

(2)为了进一步了解“懈怠性”人群中每个人的生活习惯,从步行在![]() 的人群中再随机抽取3人,求选中的人中男性人数超过女性人数的概率.
的人群中再随机抽取3人,求选中的人中男性人数超过女性人数的概率.