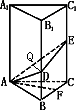
题目内容
素材1:四棱锥A-BCDE中,AD⊥底面BCDE,AE⊥BE,AC⊥BC.素材2:若∠CBE=90°,CE=![]() ,AD=1.
,AD=1.
试根据上述素材构建一个问题,然后再解答.
构建问题(一):在四棱锥A—BCDE中,AD⊥底面BCDE,AE⊥BE,AC⊥BC. 若∠CBE=90°,CE=![]() ,AD=1,试证明A、B、C、D、E都在以AB为直径的球面上.
,AD=1,试证明A、B、C、D、E都在以AB为直径的球面上.
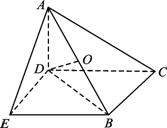
证明:连结BD,∵AD⊥底面BCDE,∴AD⊥BD.
又∵AE⊥BE,AC⊥BC,∴△ABC、△ABD、△ABE均为以AB为斜边的直角三角形,从而点A、B、C、D、E都在以AB为直径的同一球面上.
构建问题(二):在四棱锥A—BCDE中,AD⊥
底面BCDE,AE⊥BE,AC⊥BC. 若∠CBE=90°,CE=![]() ,AD=1,求B、D两点间的球面距离.
,AD=1,求B、D两点间的球面距离.
解析:取AB的中点O,则O为球心.
∵∠CBE=90°,DE为 AE在面 BCDE内的射影,AE⊥BE,
∴DE⊥BE,从而四边形BCDE为矩形.
∵CE=![]() ,∴BD=CE=
,∴BD=CE=![]() .
.
∵AD=1,∴AB=![]() =2.
=2.
从而球半径R=1.连结OD,
在△BOD中,求得∠BOD=120°=![]() ,
,
∴B、D两点间的球面距离为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 16、如图,四棱锥A-BCD被一平面所截,截面为平行四边形EFGH,求证:CD∥平面EFGH.
16、如图,四棱锥A-BCD被一平面所截,截面为平行四边形EFGH,求证:CD∥平面EFGH. (2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=
(2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=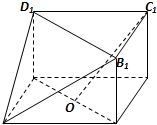 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=2,AD=4,BB1=1.
如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=2,AD=4,BB1=1.