题目内容
设锐角三角形ABC的内角A,B,C的对边分别为 ,且
,且 .
.
(1)求角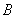 的大小;
的大小;
(2)若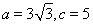 ,求
,求 的面积及
的面积及 .
.
【答案】
(1)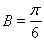 ;(2)
;(2)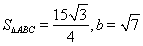 .
.
【解析】
试题分析:(1)由正弦定理,有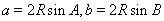 ,那么可以将条件
,那么可以将条件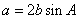 转化成角的关系:
转化成角的关系: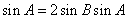 ,得到
,得到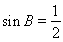 ,再由锐角三角形得到
,再由锐角三角形得到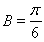 ;(2)已知
;(2)已知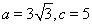 ,夹角
,夹角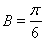 ,可直接利用正弦定理的面积公式
,可直接利用正弦定理的面积公式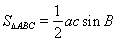 ,求出面积为
,求出面积为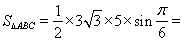
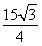 ;又由余弦定理:
;又由余弦定理: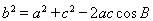 ,可得:
,可得: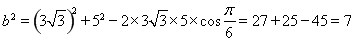 ,所以
,所以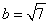 .
.
试题解析:(1)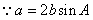 ,由正弦定理有
,由正弦定理有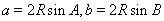 ,
,
可得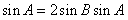 .
.
由于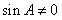 ,
,
故有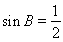
又因为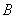 是锐角,所以:
是锐角,所以: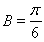 .
.
(2)依题意得: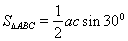
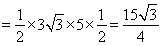 .
.
所以由余弦定理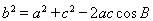 可得:
可得:
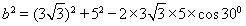
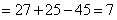 .
.
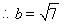
考点:正弦定理,余弦定理.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目