题目内容
1．一个多面体的三视图和直观图分别如图所示，其中M，N分别是AB，AC的中点，G是DF上的一动点．（1）求证：GN⊥AC；
（2）当FG=GD时，在边AD上是否存在一点P，使得GP∥平面FMC？
分析 （1）由已知可以判断FD⊥平面ABCD，得到FD⊥AC，结合线面垂直的判定定理得到AC⊥平面FDN，得到所证；
（2）当FG=GD时，在边AD上存在一点P，使得GP∥平面FMC，此时A，P重合．利用线面平行的庞大的灵魂证明．
解答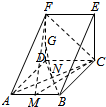 
解：（1）如图所示，由三视图可得直观图为一个横放的侧棱垂直于底面的三棱柱，且在底面ADF中，AD⊥DF，DF=AD=DC，连接DB．
可知B，N，D共线，且AC⊥DN，
又FD⊥AD，FD⊥CD，且AD∩CD=D，
所以FD⊥平面ABCD，所以FD⊥AC．
又FD∩DN=D，所以AC⊥平面FDN．
所以GN⊥AC.6分
（2）当FG=GD时，在边AD上存在一点P，使得GP∥平面FMC，此时A，P重合．
证明如下：取DC中点S，连接AS，GS，GA．
因为G是DF的中点，所以GS∥FC，AS∥CM．
又GS∩AS=S，FC∩CM=C，所以平面GSA∥平面FMC．
又GA?平面GSA，所以GA∥平面FMC，即GP∥平面FMC.12分．
点评 本题考查了线面垂直、线面平行的判定定理和性质定理的运用；熟练掌握定理并且运用定理是关键．
练习册系列答案
相关题目
12．一个空间几何体的三视图如图所示，则这个几何体的体积为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | 4 | D． | 8 |
6．
如图Rt△ABC中，∠ACB=90°，直线l过点A且垂直于平面ABC，动点P∈l，当点P逐渐远离点A时，∠PBC的大小（ ）
如图Rt△ABC中，∠ACB=90°，直线l过点A且垂直于平面ABC，动点P∈l，当点P逐渐远离点A时，∠PBC的大小（ ）| A． | 不变 | B． | 变小 | ||
| C． | 变大 | D． | 有时变大有时变小 |
如图，四棱锥P-ABCD的底面ABCD为矩形，PA⊥底面ABCD，BC=4，AB=PA=2，M为线段PC的中点，N在线段BC上，且BN=1．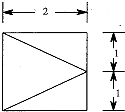
已知四棱锥，它的底面是边长为2的正方形，其俯视图如图所示，侧视图为直角三角形，则该四棱锥的侧面中直角三角形的个数有3个，该四棱锥的体积为$\frac{4}{3}$．