Question

11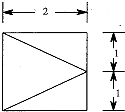．已知四棱锥，它的底面是边长为2的正方形，其俯视图如图所示，侧视图为直角三角形，则该四棱锥的侧面中直角三角形的个数有3个，该四棱锥的体积为$\frac{4}{3}$．

Answer 1

分析 根据四棱锥的俯视图得到四棱锥的特征，根据四棱锥的左视图为直角三角形，得到四棱锥的高即可求出它的体积．

解答 解：由四棱锥的俯视图可知，该四棱锥底面为ABCD为正方形，PO垂直于BC于点O，其中O为BC的中点，
若该四棱锥的左视图为直角三角形，
则△BPC为直角三角形，且为等腰直角三角形，
所以直角三角形有3个．
∵B0=1，
∴PO=BO=1，
则它的体积为V=$\frac{1}{3}$×2²×1=$\frac{4}{3}$．
故答案为：3；$\frac{4}{3}$．

点评 本题主要考查三视图的识别和应用以及锥体的体积的计算，考查线面垂直和面面垂直的判断，考查学生的推理能力．