题目内容
(1)若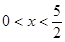 ,求
,求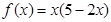 的最大值。
的最大值。
(2)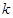 为何值时,直线
为何值时,直线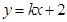 和曲线
和曲线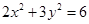 有两个公共点。
有两个公共点。
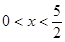 ,求
,求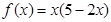 的最大值。
的最大值。(2)
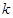 为何值时,直线
为何值时,直线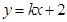 和曲线
和曲线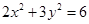 有两个公共点。
有两个公共点。(1)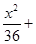
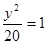 ;(2)点P的坐标为
;(2)点P的坐标为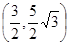 ;
;
(3)当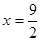 时,d取最小值
时,d取最小值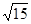 。
。
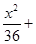
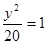 ;(2)点P的坐标为
;(2)点P的坐标为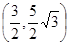 ;
;(3)当
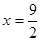 时,d取最小值
时,d取最小值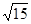 。
。试题分析: (1)根据已知条件,结合一正二定,三相等的思想来求解最值。
(2)联立方程组,根据得到的方程的解的个数得到结论。
(1)已知双曲线实半轴a1=4,虚半轴b1=2
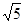 ,半焦距c1=
,半焦距c1=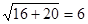 ,
,∴椭圆的长半轴a2=c1=6,椭圆的半焦距c2=a1=4,椭圆的短半轴
 =
=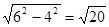 ,
,∴所求的椭圆方程为
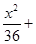
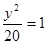 …………4分
…………4分(2)由已知
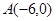 ,
,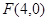 ,设点P的坐标为
,设点P的坐标为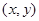 ,则
,则 由已知得
由已知得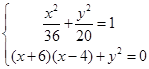 …………6分
…………6分则
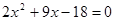 ,解之得
,解之得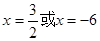 ,
, 由于y>0,所以只能取
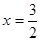 ,于是
,于是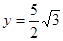 ,所以点P的坐标为
,所以点P的坐标为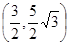 ……8分
……8分(3)直线
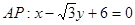 ,设点M是
,设点M是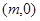 ,则点M到直线AP的距离是
,则点M到直线AP的距离是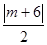 ,于是
,于是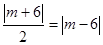 ,
,又∵点M在椭圆的长轴上,即
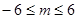
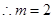 …………10分
…………10分∴当
 时,椭圆上的点到
时,椭圆上的点到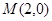 的距离
的距离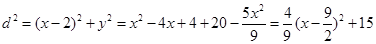
又
 ∴当
∴当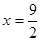 时,d取最小值
时,d取最小值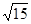 …………12分
…………12分点评:解决该试题的关键是能根据题中的条件,得到均值不等式的结构,求解最值也可以通过二次函数的性质来求解最值,同时要对于直线与双曲线的位置关系,通过联立方程组,转换为方程的解的问题来得到。

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 之间的大小关系是
之间的大小关系是



 是定义域为
是定义域为 的可导函数,且对任意实数
的可导函数,且对任意实数 都有
都有 成立.若当
成立.若当 时,不等式
时,不等式 成立,设
成立,设 ,
, ,
, ,则
,则 ,
, ,
, 的大小关系是( )
的大小关系是( )



 ,则
,则 、
、 、
、 的大小关系是
的大小关系是 



 的最小值为 .
的最小值为 . 的最小值是
的最小值是  <
< <0,已知下列不等式:①a+b<ab;②|a|>|b|;③a<b;④ a2>b2
<0,已知下列不等式:①a+b<ab;②|a|>|b|;③a<b;④ a2>b2 ,则
,则 三者的从小到大的关系为__________;
三者的从小到大的关系为__________; 的最小值等于
的最小值等于 的是( )
的是( )


