题目内容
15.若函数f(x)=x2-2x+m,在x∈[0,3]上的最大值为1,则实数m的值为-2.分析 根据二次函数的性质即可求出.
解答 解:函数f(x)=x2-2x+m=(x-1)2+m-1,其对称轴为x=1,
则f(x)在[0,1]上单调递减,在(1,3]上单调递增,
则当x=3时,函数有最大值,即为9-6+m=1,
解得m=-2,
故答案为:-2
点评 本题考查的知识点是二次函数的图象图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
7.已知m、n是两条不同的直线,α、β、γ是三个不同的平面,下列命题中正确的是( )
| A. | 若α⊥β,β⊥γ,则α∥γ | |
| B. | 若m?α,n?β,m∥n,则α∥β | |
| C. | 若m,n是异面直线,m?α,m∥β,n?β,n∥α,则α∥β | |
| D. | 平面α内有不共线的三点到平面β的距离相等,则α∥β |
20.在△ABC中,角A,B,C所对的边分别为a,b,c,cos2A=sinA,bc=2,则△ABC的面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | 2 |
4.二次函数y=-x2-4x(x>-2)与指数函数$y={(\frac{1}{2})^x}$的交点个数有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
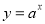 ,②
,② ,③
,③ ,④
,④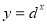 ,根据图象可得a、b、c、d与1的大小关系为( )
,根据图象可得a、b、c、d与1的大小关系为( )
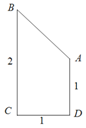 如图,直角梯形ABCD中,AD⊥DC,AD∥BC,BC=2CD=2AD=2,若将直角梯形绕BC边旋转一周,则所得几何体的表面积为$(3+{\sqrt{2}^{\;}})π$.
如图,直角梯形ABCD中,AD⊥DC,AD∥BC,BC=2CD=2AD=2,若将直角梯形绕BC边旋转一周,则所得几何体的表面积为$(3+{\sqrt{2}^{\;}})π$.