题目内容
 设F1、F2分别是椭圆
设F1、F2分别是椭圆 | x2 |
| 4 |
(1)求
| PF1 |
| PF2 |
(2)设过定点Q(0,2)的直线l与椭圆交于不同的两点M、N,且∠MON为锐角,求直线l的斜率k的取值范围.
分析:(1)由题意可求F1,F2的坐标,设P(x,y),则由向量的数量积的坐标表示可求
•
=(-
-x,-y)•(
-x,-y)结合椭圆的性质可知,-2≤x≤2,利用二次函数的性质可求•
(2)由题设条件,可设直线L:y=kx+2,M(x1,y1),N(x2,y2),联立直线与椭圆方程,由△>0可求k的范围,结合方程的根与系数关系可求x1+x2,x1x2,然后由0°<∠MON<90°可知
•
=x1x2+y1y2>0,代入可求k的范围
| PF1 |
| PF2 |
| 3 |
| 3 |
(2)由题设条件,可设直线L:y=kx+2,M(x1,y1),N(x2,y2),联立直线与椭圆方程,由△>0可求k的范围,结合方程的根与系数关系可求x1+x2,x1x2,然后由0°<∠MON<90°可知
| OM |
| ON |
解答:解:(1)由椭圆
+y2=1易知a=2,b=1,
∴c=
=
,所以F1(-
,0),F2(
,0),
设P(x,y),则
•
=(-
-x,-y)•(
-x,-y)=x2+y2-3
=x2+1-
=
由椭圆的性质可知,-2≤x≤2
∴-2≤
≤1
故-2≤
•
≤1(6分)
(2)显然直线x=0不满足题设条件,可设直线L:y=kx+2,M(x1,y1),N(x2,y2)
则
消去y,整理得:(k2+
)x2+4kx+3=0
由△=16k2-12(k2+
)>0得:k<-
或k>
…①(9分)
又∵x1+x2=-
,x1x2=
又0°<∠MON<90°
∴cos∠MON>0
∴
•
>0
∴
•
=x1x2+y1y2>0(11分)
∵y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=
+
+4=
∴
+
>0,即k2<4
∴-2<k<2…②(13分)
故由①②得-2<k<-
或
<k<2(15分)
| x2 |
| 4 |
∴c=
| a2-b2 |
| 3 |
| 3 |
| 3 |
设P(x,y),则
| PF1 |
| PF2 |
| 3 |
| 3 |
=x2+1-
| x2 |
| 4 |
| 3x2-8 |
| 4 |
由椭圆的性质可知,-2≤x≤2
∴-2≤
| 3x2-8 |
| 4 |
故-2≤
| PF1 |
| PF2 |
(2)显然直线x=0不满足题设条件,可设直线L:y=kx+2,M(x1,y1),N(x2,y2)
则
|
| 1 |
| 4 |
由△=16k2-12(k2+
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
又∵x1+x2=-
| 4k | ||
k2+
|
| 3 | ||
k2+
|
又0°<∠MON<90°
∴cos∠MON>0
∴
| OM |
| ON |
∴
| OM |
| ON |
∵y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=
| 3k2 | ||
k2+
|
| -8k2 | ||
k2+
|
| 1-k2 | ||
k2+
|
∴
| 3 | ||
k2+
|
| 1-k2 | ||
k2+
|
∴-2<k<2…②(13分)
故由①②得-2<k<-
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查了椭圆性质的应用,直线与椭圆相交关系的应用,方程的根与系数关系的应用及向量的数量积的坐标表示,属于综合试题

练习册系列答案
相关题目
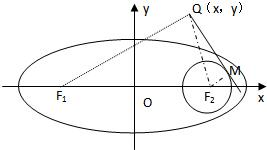 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C: