Question

【题目】已知直线的极坐标方程为，曲线的参数方程为（为参数）

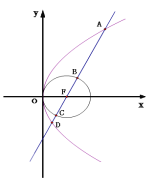
（Ⅰ）求直线的直角坐标方程和曲线的普通方程;

（Ⅱ）若过且与直线垂直的直线与曲线相交于两点，，求.

Answer 1

【答案】（Ⅰ），（Ⅱ）

【解析】

（Ⅰ）根据极坐标与直角坐标的互化公式，即可求得直线的直角坐标方程，消去参数，即可求得曲线的普通方程；

（Ⅱ）求得直线的参数方程，代入椭圆的方程，利用直线参数的几何意义，即可求解．

（Ⅰ）由直线极坐标方程为，

根据极坐标与直角坐标的互化公式，可得直线直角坐标方程：，

由曲线的参数方程为（为参数），则，

整理得，即椭圆的普通方程为．

（Ⅱ）直线的参数方程为，即（为参数）

把直线的参数方程代入得：，

故可设，是上述方程的两个实根，则有

又直线过点，故由上式及的几何意义得：.