题目内容
关于下列命题,正确的序号是 .①函数y=tanx最小正周期是π;
②函数y=cos2(
 -x)是偶函数;
-x)是偶函数;③函数y=4sin(2x-
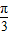 )的一个对称中心是(
)的一个对称中心是(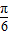 ,0);
,0);④函数y=sin(x+
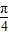 )在闭区间[-
)在闭区间[-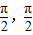 ]上是增函数.
]上是增函数.
【答案】分析:①利用周期公式可求函数y=tanx最小正周期;
②化简函数y=cos2( -x)=sin2x,可得结论;
-x)=sin2x,可得结论;
③函数y=4sin(2x-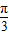 ),x=
),x=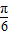 时,y=0,可得函数的一个对称中心;
时,y=0,可得函数的一个对称中心;
④函数y=sin(x+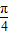 ),由x∈[-
),由x∈[-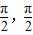 ],可得x+
],可得x+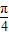 ∈
∈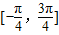 ,利用正弦函数的单调性,可得结论..
,利用正弦函数的单调性,可得结论..
解答:解:①函数y=tanx最小正周期是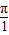 =π,故正确;
=π,故正确;
②函数y=cos2(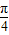 -x)=sin2x,是奇函数,故不正确;
-x)=sin2x,是奇函数,故不正确;
③函数y=4sin(2x- ),x=
),x=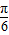 时,y=0,故函数的一个对称中心是(
时,y=0,故函数的一个对称中心是(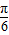 ,0),命题正确;
,0),命题正确;
④函数y=sin(x+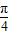 ),∵x∈[-
),∵x∈[-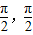 ],∴x+
],∴x+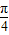 ∈
∈ ,不是增函数,故不正确.
,不是增函数,故不正确.
故答案为:①③
点评:本题考查三角函数的性质,考查学生分析解决问题的能力,属于中档题.
②化简函数y=cos2(
 -x)=sin2x,可得结论;
-x)=sin2x,可得结论;③函数y=4sin(2x-
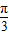 ),x=
),x=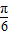 时,y=0,可得函数的一个对称中心;
时,y=0,可得函数的一个对称中心;④函数y=sin(x+
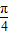 ),由x∈[-
),由x∈[-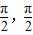 ],可得x+
],可得x+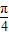 ∈
∈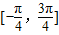 ,利用正弦函数的单调性,可得结论..
,利用正弦函数的单调性,可得结论..解答:解:①函数y=tanx最小正周期是
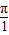 =π,故正确;
=π,故正确;②函数y=cos2(
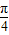 -x)=sin2x,是奇函数,故不正确;
-x)=sin2x,是奇函数,故不正确;③函数y=4sin(2x-
 ),x=
),x=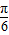 时,y=0,故函数的一个对称中心是(
时,y=0,故函数的一个对称中心是(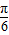 ,0),命题正确;
,0),命题正确;④函数y=sin(x+
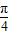 ),∵x∈[-
),∵x∈[-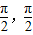 ],∴x+
],∴x+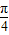 ∈
∈ ,不是增函数,故不正确.
,不是增函数,故不正确.故答案为:①③
点评:本题考查三角函数的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目