题目内容
3.已知函数f(x)是R上的增函数,它的图象经过点A(0,-2),B(3,2),则不等式|f(x+1)|≥2的解集为( )| A. | [-1,2] | B. | (-∞,-1) | C. | [2,+∞) | D. | (-∞,-1]∪[2,+∞) |
分析 由题意可得可得f(x+1)≥2,或f(x+1)≤-2,可得x+1≥3,或x+1≤0,由此求得x的范围.
解答 解:∵函数f(x)是R上的增函数,f(x)的图象经过点A(0,-2),B(3,2),
则由不等式|f(x+1)|≥2,可得f(x+1)≥2,或f(x+1)≤-2,
∴x+1≥3,或x+1≤0,求得x≥1,或 x≤-1,
故选:D.
点评 本题主要考查函数的单调性的应用,带有绝对值的函数,属于中档题.

练习册系列答案
相关题目
14.射击项目选拔赛,四人的平均成绩和方差如下表所示:
从这四个人中选择一人参加该射击项目比赛,最佳人选是( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均环数$\overline{x}$ | 8.3 | 8.8 | 8.8 | 8.7 |
| 方差s2 | 3.5 | 3.6 | 2.2 | 5.4 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
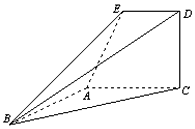 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE. 某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)
某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设∠OAB=α.(注:底面直径和高相等的圆柱叫做等边圆柱.)