题目内容
已知点M在曲线2x2-y=0上运动,点N(0,-1),点P在MN上,且NM=2NP,求点P的轨迹方程.
【答案】分析:由M在曲线2x2-y=0上运动,设M(x,2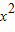 ),由N(0,-1),点P在MN上,且NM=2NP,知点P是线段MN的中点,由此能求出点P的轨迹方程.
),由N(0,-1),点P在MN上,且NM=2NP,知点P是线段MN的中点,由此能求出点P的轨迹方程.
解答:解:∵M在曲线2x2-y=0上运动,∴设M(x,2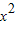 ),
),
设P(x,y),
∵N(0,-1),点P在MN上,且NM=2NP,
∴点P是线段MN的中点,
∴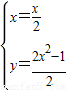 ,整理,得8x2-2y-1=0.
,整理,得8x2-2y-1=0.
∴点P的轨迹方程是8x2-2y-1=0.
点评:本题考查点的轨迹方程的求法,是基础题.解题时要认真审题,仔细解答,注意中点坐标公式的合理运用.
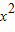 ),由N(0,-1),点P在MN上,且NM=2NP,知点P是线段MN的中点,由此能求出点P的轨迹方程.
),由N(0,-1),点P在MN上,且NM=2NP,知点P是线段MN的中点,由此能求出点P的轨迹方程.解答:解:∵M在曲线2x2-y=0上运动,∴设M(x,2
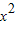 ),
),设P(x,y),
∵N(0,-1),点P在MN上,且NM=2NP,
∴点P是线段MN的中点,
∴
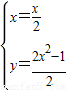 ,整理,得8x2-2y-1=0.
,整理,得8x2-2y-1=0.∴点P的轨迹方程是8x2-2y-1=0.
点评:本题考查点的轨迹方程的求法,是基础题.解题时要认真审题,仔细解答,注意中点坐标公式的合理运用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目