题目内容
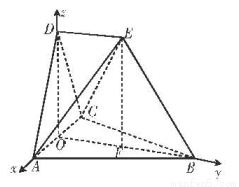
(本题满分12分)在如图所示的空间几何体中,平面 平面ABC,
平面ABC,
AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
 的平分线上。
的平分线上。

(1)求证:DE//平面ABC;
(2)求二面角E—BC—A的余弦值;
【答案】
解:方法一:(1)由题意知, 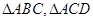 都是边长为2的等边三角形,
都是边长为2的等边三角形,
取AC中点O,连接BO,DO,
则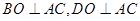
 平面ACD
平面ACD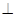 平面ABC
平面ABC
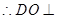 平面ABC,作EF
平面ABC,作EF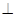 平面ABC,
平面ABC,
那么EF//DO,根据题意,点F落在BO上,
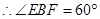 ,易求得
,易求得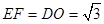
所以四边形DEFO是平行四边形,DE//OF;
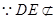 平面ABC,
平面ABC,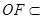 平面ABC,
平面ABC,
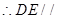 平面ABC…………6分
平面ABC…………6分
(2)作FG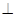 BC,垂足为G,连接FG;
BC,垂足为G,连接FG;
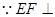 平面ABC,根据三垂线定理可知,EG
平面ABC,根据三垂线定理可知,EG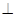 BC
BC
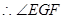 就是二面角E—BC—A的平面角
就是二面角E—BC—A的平面角
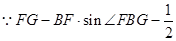
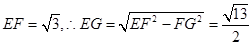
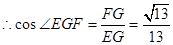
即二面角E—BC—A的余弦值为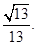 …………12分
…………12分
方法二:(1)同方法一
(2)建立如图所示的空间直角坐标系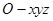 ,
,
可求得平面ABC的一个法向量为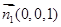 ,
,
平面BCE的一个法向量为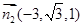
所以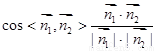
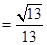
又由图知,所求二面角的平面角是锐角,所以二面
角E—BC—A的余弦值为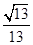 ;…12分
;…12分
【解析】略

练习册系列答案
相关题目
 中
中 分别为A,B,C所对的边,
分别为A,B,C所对的边, 且
且

 ,求
,求 的取值范围
的取值范围 中,数列的前n项和
中,数列的前n项和 满足
满足
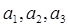 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列 中,E是BC的中点,F是
中,E是BC的中点,F是 的中点
的中点
 的平面角的余弦值。
的平面角的余弦值。