题目内容
在△ABC中，若sinA=
，则△ABC是（ ）三角形．A．等腰
B．等腰直角
C．直角
D．等边
【答案】分析：利用正弦定理及余弦定理可得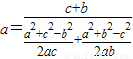
，整理可得a，b，c的关系，进而判断三角形的形状．
解答：解：由已知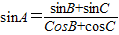
，利用正弦定理及余弦定理可得
∴
∴
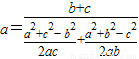
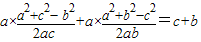
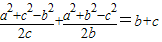
∴b（a2+c2-b2）+（a2+b2-c2）c=2bc2+2b2c
∴a2（b+c）-（c+b）（b2+c2-bc）=（b+c）bc
∴a2=b2+c2
△ABC是直角三角形
故选C
点评：本题主要考查了综合利用正弦定理及余弦定理判断三角形的形状，利用正弦定理把“角”转化为“边”时，常用的一些结论 ①a=2RsinA，b=2RsinB，c=2RsinC（R为三角形外接圆的半径）
②sinA=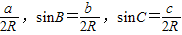
③a：b：c=sinA：sinB：sinC
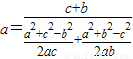，整理可得a，b，c的关系，进而判断三角形的形状．解答：解：由已知
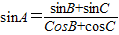，利用正弦定理及余弦定理可得∴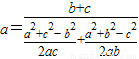
∴
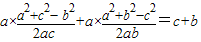
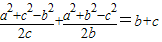
∴b（a2+c2-b2）+（a2+b2-c2）c=2bc2+2b2c
∴a2（b+c）-（c+b）（b2+c2-bc）=（b+c）bc
∴a2=b2+c2
△ABC是直角三角形
故选C
点评：本题主要考查了综合利用正弦定理及余弦定理判断三角形的形状，利用正弦定理把“角”转化为“边”时，常用的一些结论 ①a=2RsinA，b=2RsinB，c=2RsinC（R为三角形外接圆的半径）
②sinA=
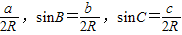③a：b：c=sinA：sinB：sinC 
练习册系列答案
相关题目
在△ABC中，若sinA：sinB：sinC=5：7：8，则此三角形的最大角与最小角之和为（ ）
| A、90° | B、120° | C、135° | D、150° |